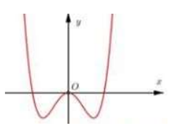
Cho hàm số có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng sao cho từ đó kẻ được hai tiếp tuyến đến (C).
A. 4 điểm
B. 2 điểm
C. 3 điểm
D. 1 điểm
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Phương pháp:
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
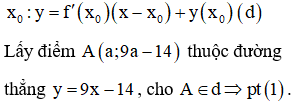
Để từ A kẻ được hai tiếp tuyến đến (C) thì phương trình (1) có 2 nghiệm phân biệt. Tìm điều kiện của a để phương trình có 2 nghiệm phân biệt. Có bao nhiêu giá trị của a thì có bấy nhiêu điểm thỏa mãn yêu cầu bài toán.

Cách giải:
TXĐ : D = R.
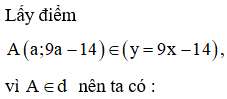
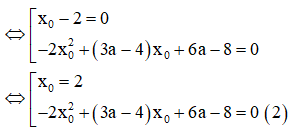
Để qua A kẻ được 2 tiếp tuyến đến đồ thị (C) thì phương trình (1) có 2 nghiệm phân biệt.
TH1 : là nghiệm của phương trình (2) ta có :

TH2 : không là nghiệm của phương trình (2), khi đó để (1) có 2 nghiệm phân biệt thì (2) có nghiệm kép khác 2.
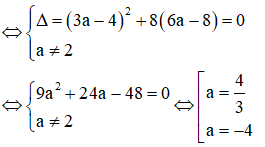
Vậy có 3 giá trị của a thỏa mãn yêu cầu bài toán.
Chú ý và sai lầm: Cần phải làm hết các trường hợp để phương trình (1) có 2 nghiệm, tránh trường hợp thiếu TH1 và chọn nhầm đáp án B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với đáy. Mệnh đề nào sau đây sai?
Có bao nhiêu số tự nhiên có 5 chữ số, các chữ số khác 0 và đôi một khác nhau
Thể tích của khối chóp có diện tích đáy bằng S và chiều cao bằng h là:
Gọi S là tập nghiệm của phương trình trên R. Tổng các phần tử của S bằng
Với mọi số thực dương a, b, x, y và , mệnh đề nào sau đây sai?
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?
Biết hình dưới đây là đồ thị của một trong bốn hàm số sau, hỏi đó là đồ thị hàm số nào?