Xét hàm số , với m là tham số thực. Có bao nhiêu số nguyên thỏa mãn điều kiện ?
A. 6
B. 7
C. 4
D. 5
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Nhận thấy f(x) liên tục trên [-1;3] nên tồn tại giá trị nhỏ nhất của f(x) trên đoạn [-1;3].
Ta có nên suy ra .
Vậy điều kiện .
Ta có Phương trình vô nghiệm trên [-1;3]
Phương trình vô nghiệm trên
Xét hàm số
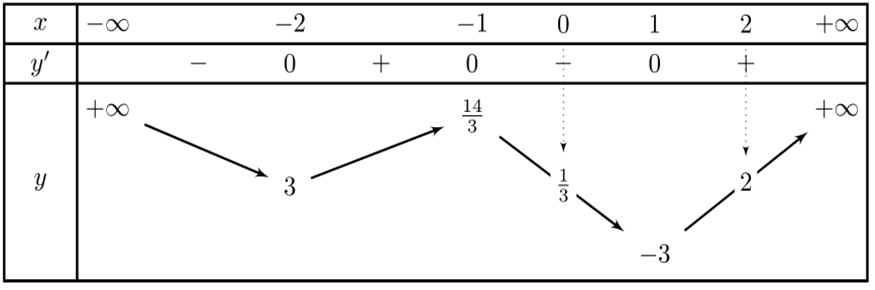
Bảng biến thiên
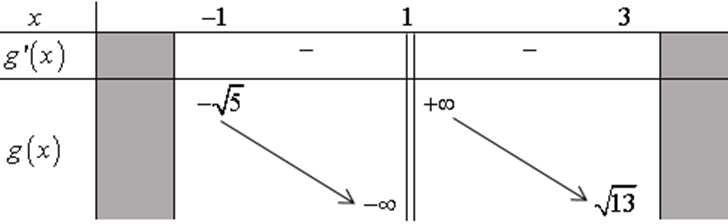
Từ bảng biến thiên suy ra điều kiện phương trình vô nghiệm trên .
Do m nguyên nên .
Để giải (2) trước hết ta đi tìm điều kiện để .
Do f(1)=2 nên , mà , suy ra x=1 là điểm cực trị của hàm số f(x)
Đặt .
Do đó với m nguyên thì (2) chắc chắn xảy ra.
Vậy thỏa mãn điều kiện (2)
Kết luận: Có 6 giá trị nguyên của m thỏa mãn yêu cầu.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Biết rằng đồ thị hàm số có hai điểm cực trị là A(0;2) và B(2;-14). Khi đó f(3) bằng
Cho hàm số . Số giá trị nguyên của m để hàm số nghịch biến trên là
Một đoàn khách có 8 người bước ngẫu nhiên vào một cửa hàng có 3 quầy. Xác suất đề quầy thứ nhất có 3 khách ghé thăm là
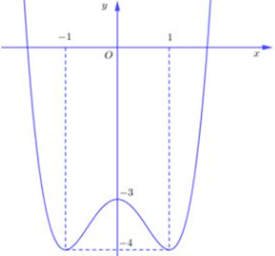
Cho hàm số f(x) có đồ thị như hình vẽ. Số giá trị nguyên dương của tham số m để phương trình có 2 nghiệm là
Cho hàm số y=f(x) xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
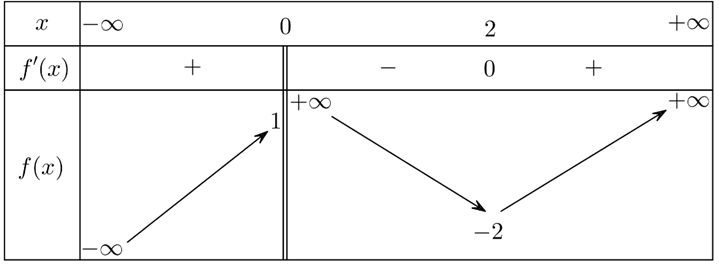
Tập hợp tất cả các giá trị của tham số thực m sao cho phương trình có đúng nghiệm thực phân biệt là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông; hình chiếu của S trên (ABCD) trùng với trung điểm H của cạnh AB; kí hiệu là diện tích của hình vuông ABCD. Công thức tính thể tích của khối chóp S.ABCD là
Cho hàm số có bảng biến thiên như sau :
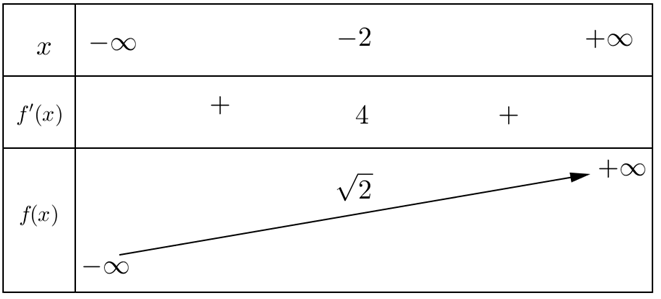
Có bao nhiêu số dương trong các hệ số a,b,c?
Cho hàm số y=f(x) có bảng biến thiên như sau
Số nghiệm thuộc đoạn của phương trình là