Trong không gian Oxyz, cho hình nón có đỉnh I thuộc mặt phẳng và hình tròn đáy nằm trên mặt phẳng . Mặt phẳng (Q) đi qua điểm A(0;-2;0) và vuông góc với trục của hình nón chia hình nón thành hai phần có thể tích lần lượt là và ( là thể tích của hình nón chứa đỉnh I). Biết bằng biểu thức đạt giá trị nhỏ nhất khi , . Khi đó tổng bằng
C. 2031
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
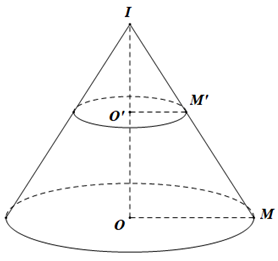
Dễ thấy , gọi O là tâm của đường tròn đáy hình nón, , từ giả thiết ta có
; suy ra OO'=2IO'.
Gọi M là điểm thuộc đường tròn (O), , do nên .
Do đó , (trong đó và lần lượt là bán kính của các đường tròn (O') và (O)). Đặt , khi đó
.
Dấu "=" xảy ra khi . Suy ra .
Vậy .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chọn ngẫu nhiên 2 viên bi từ một hộp chứa 2 viên bi đỏ và 3 viên bi xanh. Xác suất để chọn được 2 viên bi xanh là
Khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng . Thể tích khối nón đã cho là
Cho đồ thị hàm số y=f(x) như hình vẽ bên
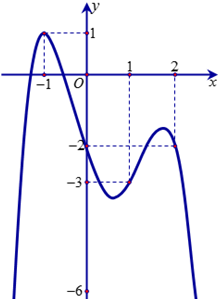
Số điểm cực đại, cực tiểu của hàm số là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy (ABCD). Thể tích khối chóp S.ABCD là
Cho a là một số dương, biểu thức viết dưới dạng lũy thừa với số mũ hữu tỉ là
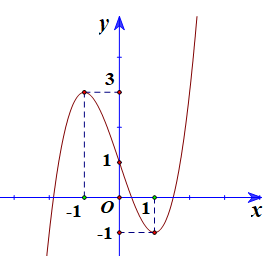
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai mặt phẳng (BCD'A') và (ABCD) bằng