Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Giả sử BC = AH = a
Vì ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc B và góc C.
Cho tam giác ABC có = 60o, = 55o, AC = 3,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
Cho tam giác ABC có = 70o, = 35o, AC = 4,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)
Tứ giác ABCD có = 90o, = 45o, AB = 6cm, AD = 8cm. Tính diện tích tứ giác ABCD
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính cos và chu vi tam giác ABH.
Cho tam giác ABC vuông cân tại A (AB = AC = a). Phân giác của góc B cắt AC tại D. Tính DA; DC theo a
Cho tam giác ABC cân tại A, = 65o, đường cao CH = 3,6. Hãy giải tam giác ABC
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết = 60o, CH = a. Tính độ dài AB và AC theo a
Cho hình thang ABCD vuông tại A và D; = 50o. Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD
Tứ giác ABCD có = 90o, = 40o, AB = 4cm, AD = 3cm. Tính diện tích tứ giác ABCD (làm tròn đến chữ số thập phân thứ hai).
Cho tam giác ABC vuông tại A; BC = a không đổi,
Lập công thức để tính diện tích tam giác ABC theo a và
Cho tam giác ABC vuông tại A; BC = a không đổi
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy
Các hệ thức trong tam giác vuông:
Định lí. Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.
+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với côtang của góc kề.
Ví dụ. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c.
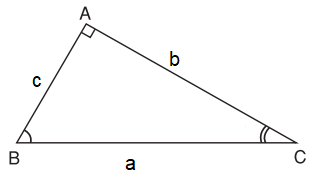
Khi đó, a là độ dài cạnh huyền;
b và c là độ dài hai cạnh góc vuông.
Do đó: b = a.sin B = a.cos C; c = a.sin C = a.cos B;
b = c.tan B = c.cot C; c = b.tan C = b.cot C.