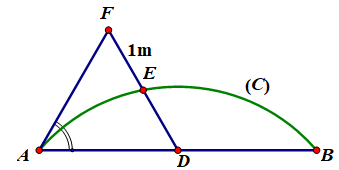
Mặt tiền nhà ông An có chiều ngang AB=4m, ông An muốn thiết kế lan can nhô ra có dạng là một phần của đường tròn (C) (hình vẽ). Vì phía trước vướng cây tại vị trí F nên để an toàn, ông An cho xây đường cong cách 1m tính từ trung điểm D của AB. Biết AF=2m, và lan can cao 1m làm bằng inox với giá 2,2 triệu/m2. Tính số tiền ông An phải trả (làm tròn đến hàng ngàn).
A. 7,568,000
B. 10,405,000
C. 9,977,000
D. 8,124,000
 Giải bởi Vietjack
Giải bởi Vietjack
Theo giả thiết, ta có đều nên FD=2m suy ra ED=1m, và .
Trong tam giác có .
Gọi R là bán kính của đường tròn (C) tâm O, áp dụng định lý sin trong tam giác ta có , suy ra .
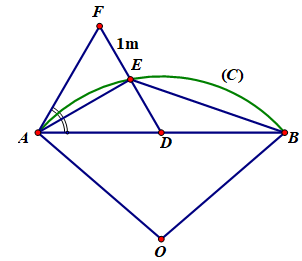
Xét tam giác OAB có , AB=4, suy ra .
Khi đó , suy ra độ dài dây cung (C) xấp xỉ 4,54m.
Vì chiều cao của lan can là 1m và giá kính là 2,2 triệu/m2 nên số tiền ông An phải trả xấp xỉ 9,977,000đ.
Chọn C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC có đáy ABC là tam giác đều, . Mặt phẳng (SBC) cách A một khoảng bằng a và hợp với mặt phẳng (ABC) một góc . Thể tích của khối chóp S.ABC bằng
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, chiều cao bằng . Khoảng cách từ B đến mặt phẳng (SCD) bằng
Cho hàm số f(x)=sin3x. Trong các khẳng định sau, khẳng định nào đúng?
Chọn ngẫu nhiên hai số bất kì trong 10 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là số lẻ?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tan góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
Trong không gian Oxyz, đường thẳng đi qua A(-1;1;3) và vuông góc với mặt phẳng có phương trình tham số là
Trong không gian hệ tọa độ Oxyz, cho hai điểm A(0;3;0), B(0;-3;0). Mặt cầu (S) nhận AB là đường kính. Hình trụ (H) là hình trụ có trục thuộc trục tung, nội tiếp với mặt cầu và có thể tích lớn nhất. Khi đó mặt phẳng chứa đáy của hình trụ đi qua điểm nào sau đây?