Cho hàm số $y=a{x}^3+b{x}^2+cx+d$. Hàm số luôn đồng biến trên $\mathrm{ℝ}$ khi và chỉ khi

Tập xác định của hàm số $y={\log }_3\left(4-x\right)$ là

Cho f(x), g(x) là các hàm số xác định và liên tục trên $\mathrm{ℝ}$. Trong các mệnh đề sau, mệnh đề nào sai?

Cho hàm số $y=\frac{2020}{x-2}$ có đồ thị (H). Số đường tiệm cận của (H) là?

Người ta muốn chia tập hợp 16 học sinh gồm 3 học sinh lớp 12A, 5 học sinh lớp 12B và 8 học sinh lớp 12C thành hai nhóm, mỗi nhóm có 8 học sinh. Xác suất sao cho ở mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B là:

Cho khối tứ diện ABCD có thể tích 2020. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.

Cho hình trụ có bán kính đáy bằng 3 cm, độ dài đường cao bằng 4 cm. Tính diện tích xung quanh của hình trụ này?

Cho b là số thực dương khác 1. Tính $P={\log }_b\left(b^2.b^{\frac{1}{2}}\right)$.

Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng

Trong không gian Oxyz, cho hai điểm A(-1;2;1) và B(2;1;0). Mặt phẳng qua A và vuông góc với AB có phương trình là

Cho hàm số $f\left(x\right)=\left|x^4-4x^3+4x^2+a\right|$. Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên [0;2]. Có bao nhiêu số nguyên a thuộc [-4;4] sao cho $M\le 2m$?

Gọi $z_1$ là nghiệm phức có phần ảo dương của phương trình $z^2+6z+13=0$. Tìm tọa độ điểm M biểu diễn số phức $w=\left(i+1\right)z_1$

Một người tham gia chương trình bảo hiểm HÀNH TRÌNH HẠNH PHÚC của công ty Bảo Hiểm MANULIFE với thể lệ như sau: Cứ đến tháng 9 hàng năm người đó đóng vào công ty là 12 triệu đồng với lãi suất hàng năm không đổi là 6%/ năm. Hỏi sau đúng 18 năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân

Cho hình nón tròn xoay có chiều cao h=20(cm), bán kính đáy r=25(cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12(cm). Tính diện tích của thiết diện đó

Cho hàm số y=f(x) có bảng biến thiên như hình bên. Số nghiệm của phương trình $f\left(x\right)+3=0$ là:

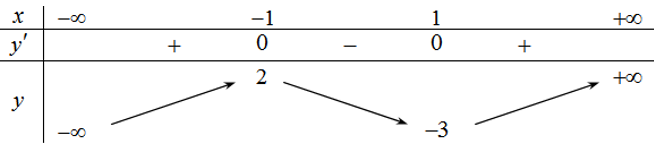
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên:

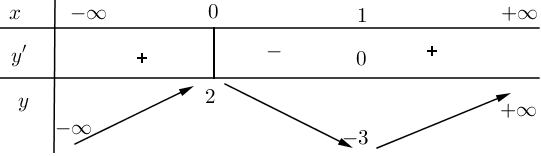
Khẳng định nào sau đây là khẳng định đúng: