Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(3;-1;1); B(-5;3;-1) và đường thằng $d:\frac{x-m}{2}=\frac{y-n}{1}=\frac{z+1}{-p}$, trong đó m,n,p>1 là những số thực và n>1. Biết rằng tồn tại vô số mặt phẳng chứa d đồng thời cách đều hai điềm A và B. Giá trị nhỏ nhất của T=m+n+p bằng

Cho khối chóp có diện tích đáy bằng S và thể tích bằng V. Khoảng cách từ đỉnh chóp đến đáy chóp bằng

Cho các số thực $x>1>y>0$. Hãy chọn đáp án đúng trong các đáp án dưới đây?

Cho hình chóp S.ABC có $SC=a\sqrt{2}$, tam giác SAB đều cạnh a và tam giác SAC vuông tại A. Mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Thể tích khối cầu ngoại tiếp hình chóp SABC là

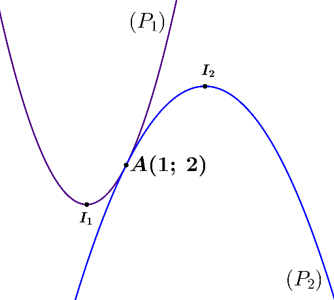
Cho hai parabol $\left(P_1\right)$ và $\left(P_2\right)$ tiếp xúc với nhau như hình vẽ. Biết tọa độ đỉnh của hai parabol $\left(P_1\right)$ và $\left(P_2\right)$ lần lượt là $I_1\left(0;1\right)$ và $I_1\left(0;1\right)$ Biết phương trình của parabol $\left(P_2\right)$  là: $y=a{x}^2+bx+c.$ Hỏi giá trị của biểu thức $P=a+b+3c$ bằng bao nhiêu ?

Cho khối nón (N) có chiều cao bằng $\sqrt{3}$ lần bán kính đáy. Dùng một mặt phẳng vuông góc với đường cao của (N) để chia (N) thành hai phần có thể tích bằng nhau . Hỏi tỉ lệ diện tích toàn phần của phần chứa đỉnh nón so với diện tích toàn phần của phần không chứa đỉnh nón bằng bao nhiêu ? 

Cho hình chóp tứ giác đều S.ABCD, có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Gọi M là điểm nằm trên cạnh AB sao cho MA=2MB. Khoảng cách giữa hai đường thẳng SM và CD bằng

Cho phương trình ${\log }^{2}x-\log \left(10x^4\right)+10-m=0$. Hãy tìm tất cả các giá trị thực của tham số  để phương trình đã cho có hai nghiệm phân biệt ?

Tích phân $\underset{0}{\overset{2019}{\int }}{e}^{x}dx$ có giá trị bằng

Một vật đang chuyển động thẳng với tốc độ $v_0=20m/s$ thì ở thời điểm $t_1$ chịu tác dụng của một lực hãm và có gia tốc $a=1-2t\left(m/s^2\right)$. Quãng đường vật đi được tính từ $t_1$ cho đến khi vật dừng lại là: 

Cho tập S gồm các số tự nhiên không vượt quá ${10}^7$ và có các chữ số được chọn từ hai số $\left\{1;2\right\}$. Chọn ngẫu nhiên từ tập S hai số. Tính xác suất để cả hai số đều chia hết cho 18?

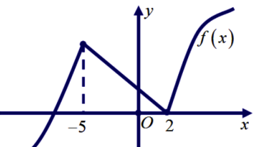
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hàm số f(x) nghịch biến trên

Cho cấp số nhân có công sai bằng 2 và số hạng đầu bằng 3. Số hạng thứ 3 bằng

Họ nguyên hàm của hàm số $f\left(x\right)=3.e^{2\ln x}$ với x>0 là

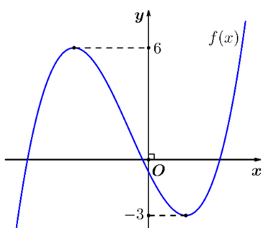
Cho hàm số y=f(x) có đồ thị như hình vẽ. Gọi S là tập chứa tất cả giá trị nguyên của m để hàm số $y=\left|f\left(x\right)+2m–3\right|$ có 5 điểm cực trị . Số phần tử của S là

Nếu chỉ xét các đường tiệm cận đứng và tiệm cận ngang thì tổng số đường tiệm cận của đồ thị hàm số $y=\sqrt{x^2-2x}-x+\frac{1}{x^2-1}$ bằng