Cho biểu thức . Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.
 Giải bởi Vietjack
Giải bởi Vietjack
Vì . Do đó ta tìm để
Vì nên để thì
Ta có bảng:
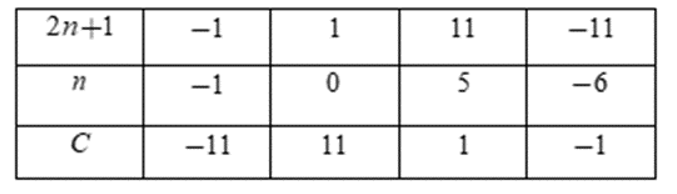
Vì nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho các phân số:
Số cặp phân số bằng nhau trong những phân số trên là:
Cho tập A={1; −2; 3; 4}. Có bao nhiêu phân số có tử số và mẫu số thuộc A mà có tử số khác mẫu số và tử số trái dấu với mẫu số?
1. Khái niệm phân số
Kết quả của phép chia số nguyên a cho số nguyên b khác 0 có thể viết dưới dạng
Ta gọi là phân số.
Phân số đọc là: a phần b, a là tử số (còn gọi tắt là tử), b là mẫu số (còn gọi tắt là mẫu).
Ví dụ 1. Kết quả của phép chia 5 cho 12 có thể viết dưới dạng
Ta gọi là phân số và đọc là năm phần mười hai; trong đó 5 là tử số, 12 là mẫu số.
Chú ý: Mọi số nguyên a có thể viết dưới dạng phân số là
Ví dụ 2. Số ‒2 có thể viết dưới dạng phân số là
Số 30 có thể viết dưới dạng phân số là
2. Phân số bằng nhau
Khái niệm hai phân số bằng nhau: Hai phân số được gọi là bằng nhau nếu chúng cùng biểu diễn một giá trị.
Quy tắc bằng nhau của hai phân số:
Xét hai phân số và .
Nếu thì a.d = b.c. Ngược lại, nếu a.d = b.c thì .
Ví dụ 3. Hai phân số trong mỗi trường hợp sau có bằng nhau không?
a) và ;
b) và .
Hướng dẫn giải
a) và
Ta so sánh hai tích (‒1).9 và 3.(‒3)
(‒1).9 = ‒9 và 3.(‒3) = ‒9
Do đó (‒1).9 = 3.(‒3).
Suy ra .
Vậy .
b) và
Ta so sánh hai tích (‒4).15 và (‒10).(‒6)
(‒4).15 = ‒60 và (‒10).(‒6) = 60
Do đó (‒1).9 ≠ 3.(‒3).
Vậy hai phân số và không bằng nhau.
Suy ra .
Vậy .
Chú ý: Với a, b là hai số nguyên và b ≠ 0, ta luôn có: và .
Ví dụ 4.
3. Tính chất cơ bản của phân số
a) Tính chất cơ bản
- Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
với , m ≠ 0.
- Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
với m ƯC(a, b).
Ví dụ 5.
a) ;
b) .
Chú ý: Mỗi phân số đều đưa được về một phân số bằng nó và có mẫu là số dương.
Ví dụ 6. (với ).
b) Rút gọn về phân số tối giản
Dựa vào tính chất cơ bản của phân số, để rút gọn phân số với tử và mẫu là số nguyên về phân số tối giản ta thường làm như sau:
Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu “– “ (nếu có)
Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất (ƯCLN) vừa tìm được, ta có phân số tối giản cần tìm.
Ví dụ 7. Rút gọn mỗi phân số sau về phân số tối giản có mẫu số là số dương.
a) ;
b)
Hướng dẫn giải
a)
Ta có ƯCLN(12, 27) = 3. Do đó .
b)
Ta có ƯCLN(36, 42) = 6. Do đó
c) Quy đồng mẫu nhiều phân số
Để quy đồng nhiều phân số, ta thường làm như sau:
Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm bội chung nhỏ nhất (BCNN) của các mẫu dương đó để làm mẫu số chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.
Ví dụ 8. Quy đồng mẫu những phân số sau:
a) và ;
b) ; và ` .
Hướng dẫn giải
a) và ;
BCNN(6, 5) = 30.
Ta có: 30 : 6 = 5 và 30 : 5 = 6.
Vậy và .
b) ; và .
Ta có và .
BCNN(6, 12, 18) = 36.
Mà 36 : 6 = 6; 36 : 12 = 3 và 36 : 18 = 2.
Vậy và