Trong không gian hệ tọa độ Oxyz, cho các điểm A(a;0;0). B(0;b;0), C(0;0;c) với a≥4,b≥5,c≥6 và mặt cầu (S) có bán kính bằng 3√102 ngoại tiếp tứ diện O.ABC. Khi tổng OA+OB+OC đạt giá trị nhỏ nhất thì mặt phẳng (α) đi qua tâm I của mặt cầu (S) và song song với mặt phẳng (OAB) có dạng mx+ny+pz+q=0 ( với m,n,p,q∈ℤ;qp là phân số tối giản). Giá trị T = m + n + p + q bằng
A. 3
B. 9
C. 5
D. -5
Giải bởi Vietjack
Chọn D
Bán kính mặt cầu ngoại tiếp tứ diện OABC là R=√a2+b2+c22=3√102⇔a2+b2+c2=90.
Ta có P=OA+OB+OC=a+b+c. Đặt x=a−4≥0,y=b−5≥0,z=c−6≥0.
Khi đó a2+b2+c2=(x+4)2+(y+5)2+(z+6)2=x2+y2+z2+8x+10y+12z+77=90.
⇒x2+y2+z2+8x+10y+12z=13.
T=(x+y+z)2+12(x+y+z)=x2+y2+z2+8x+10y+12z+2(xy+yz+zx+2x+y).
Vì x2+y2+z2+8x+10y+12z=13 và x,y,z≥0 nên (x+y+z)2+12(x+y+z)−13≥0.
⇔x+y+z≥1⇔a−4+b−5+c−7≥1⇔a+b+c≥16⇒{OA+OB+OC}min=16.
Dấu “ = ” xảy ra khi và chỉ khi a=4,b=5,c=7.
Suy ra, A(4;0;0),B(0;5;0),C(0;0;7).
Gọi mặt cầu (S):x2+y2+z2−2ax−2by−2cz+d=0
Vì A(4;0;0),B(0;5;0),C(0;0;7),O(0;0;0) nên ta có hệ
{16−8a+d=025−10b+d=047−14z+d=0d=0⇔{a=2b=52c=72d=0
Tâm của mặt cầu (S) là I(2;52;72).
Mặt phẳng (α) song song với mặt phẳng (OAB)≡(Oxy):z=0⇒(α):z+e=0.
Vì I(2;52;72) thuộc (α) nên 72+e=0⇔e=−72
Suy ra, 2z−7=0⇒m=0;n=0;p=2;q=−7.
T= m + n + p + q = -5
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho f(x) là hàm bậc bốn thỏa mãn f(0)=0. Hàm số f'(x) có đồ thị như hình vẽ
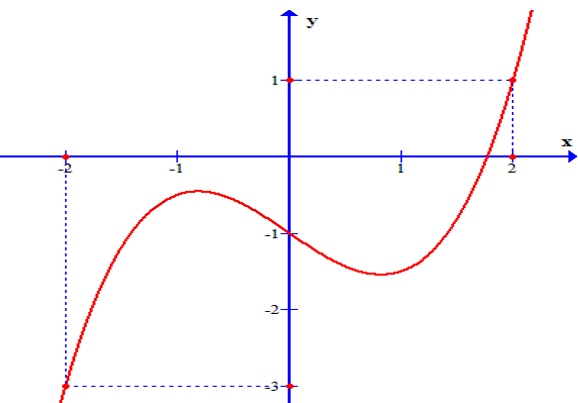
Hàm số g(x)=|2f(x2+x)−x4−2x3+x2+2x| có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) có bảng biến thiên như sau:
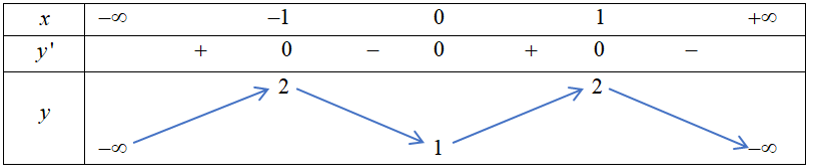
Giá trị cực tiểu của hàm số đã cho bằng
Cho hàm số f(x) xác định trên R và có đồ thị f=(x) như hình vẽ bên dưới. Giá trị nhỏ nhất của hàm số g(x)=f(2x)−2x+1 trên đoạn [−12;1] bằng
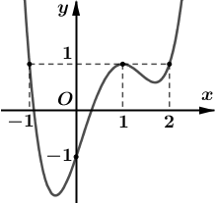
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [2;4], biết f(2)=5 và f(4)=21. Tính I=4∫2[2f'
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Xác suất để mặt 3 chấm xuất hiện là
Có bao nhiêu số nguyên y sao cho với mỗi không có quá 50 số nguyên x thoả mãn bất phương trình sau: ?
Trong không gian Oxyz, cho hai điểm A(-2;1;1), B(0;-1;1). Phương trình mặt cầu đường kính AB là:
Cho hàm số bậc ba y=f(x) có đồ thị (C) là đường cong trong hình bên. Biết hàm số f(x) đạt cực trị tại hai điểm thỏa mãn và . Gọi d là đường thẳng đi qua hai điểm cực trị của đồ thị (C). Diện tích hình phẳng giới hạn bởi (C) và d ( phần được tô đậm trong hình) bằng
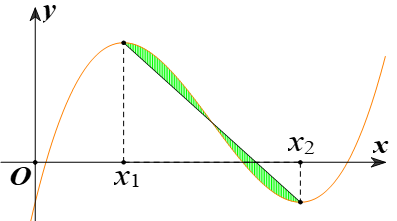
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số .
Một khối nón tròn xoay có độ dài đường sinh l=10cm và bán kính đáy r=8cm. Khi đó thể tích khối nón là:
