Tích vô hướng của hai véctơ $\overrightarrow{a}(-2;2;5), \overrightarrow{b}(0;1;2)$ trong không gian bằng

Tính a+b+c, biết tồn tại duy nhất bộ các số nguyên a, b, c để ${\int }_2^3$(4x+2)ln xdx=a+bln2+c ln3. Giá trị của a+b+c bằng

Cho hình lăng trụ ABC.A'B'C'. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA', BB', CC'  sao cho AM=2MA', NB'=2NB, PC=PC'. Gọi V₁,V₂ lần lượt là thể tích của hai khối đa diện ABCMNP và A'B'C'MNP. Tính tỷ số $\frac{V_1}{V_2}$.

Trong không gian Oxyz, cho mặt cầu (S): (x-2)²+(y-5)²+(z-3)² =27 và đường thẳng $d:\frac{x-1}{2}=\frac{y}{1}=\frac{z-2}{2}$. Mặt phẳng (P) chứa đường thẳng d và cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Nếu phương trình của (P) là ã+by-z+c=0 thì

Cho hai số phức z₁,z₂ thỏa mãn |z₁-3i+5|=2 và |iz₂-1+2i|=4. Tìm giá trị lớn nhất của biểu thức T=|2iz₁+3z₂|.

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=\frac{\sin x+ \cos x}{2 \sin x- \cos x+3}$ lần lượt là:

Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, góc giữa mặt bên và mặt phẳng đáy là $\alpha$ thỏa mãn $\cos \alpha =\frac{1}{3}$. Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỷ số thể tích của hai khối đa diện (khối bé chia khối lớn) bằng

Trong không gian tọa độ Oxyz, cho mặt cầu (S): x²+y²+z²+4x-6y+m=0 và đường thẳng Δ là giao tuyến của hai mặt phẳng $\left(\alpha \right):x+2y-2z-4=0 và ( \beta ): 2x-y-z+1=0$. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn  AM=8 khi:

Một kĩ sư được nhận lương khởi điểm là 8.000.000 đồng/tháng. Cứ sau 2 năm lương mỗi tháng của kĩ sư đó được tăng thêm 10% so với mức lương hiện tại. Tính tổng số tiền T (đồng) kĩ sư đó nhận được sau 6 năm làm việc.

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+(y-1)²+z²=4 và một điểm M(2;3;1). Từ M kẻ được vô số các tiếp tuyến tới (S), biết tập hợp các tiếp điểm là đường tròn (C). Tính bán kính r của đường tròn SC.

Gọi z₁,z₂ là hai nghiệm phức của phương trình z²+6z+13=0 trong đó z₁ là số phức có phần ảo âm. Tìm số phức $\omega =z_1+2z_2$.

Tính tổng T của tất cả các nghiệm của phương trình 4.9^x-13.6^x+9.4^x=0?

Cho hàm số y=x³-3x² có đồ thị (C) và điểm M(m;-4).Hỏi có bao nhiêu số nguyên m thuộc đoạn [-10;10] sao cho qua điểm M có thể kẻ được ba tiếp tuyến đến (C).

Cho hàm số f(x) liên tục trên $\mathrm{ℝ}$ và có bảng biến thiên như hình bên.

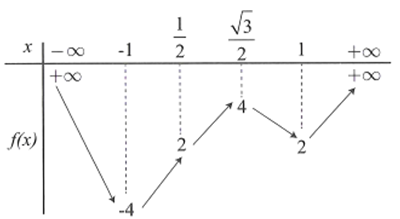
Số giá trị nguyên của tham số m để phương trình f²(cos x)+ (3-m) f(cos x)+2m 10=0 có đúng 4 nghiệm phân biệt thuộc đoạn $\left[-\frac{\mathrm{\pi }}{3};\mathrm{\pi }\right]$ là

Trong không gian Oxyz, cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1) và mặt phẳng $\left(\alpha \right)$ có phương trình 2x+2y+z-3=0. Biết rằng tồn tại duy nhất điểm M(a;b;c) thuộc mặt phẳng $\left(\alpha \right)$ sao cho MA=MB=MC. Đẳng thức nào sau đây đúng?

Cho hàm số f(x)=x³-(2m+1)x²+3mx-m có đồ thị (C_m). Có bao nhiêu giá trị nguyên của tham số m thuộc (-2018; 2018] để đồ thị (C_m) có hai điểm cực trị nằm khác phía so với trục hoành.