Cho đa giác có 20 đỉnh. Chọn 4 đỉnh bất kì của đa giác. Tính xác suất để 4 đỉnh được chọn tạo thành một tứ giác có đúng 2 cạnh chung với đa giác.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Số cách chọn 4 đỉnh từ 20 đỉnh là: .
Gọi A là biến cố 4 đỉnh được chọn tạo thành tứ giác có đúng 2 cạnh chung với đa giác.
Số tứ giác có 2 cạnh chung với đa giác n đỉnh có công thức là: .
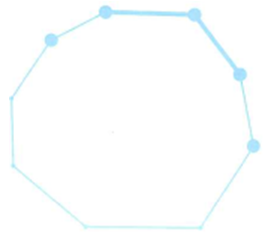
Trường hợp 1: Tứ giác có hai cạnh kề trùng với cạnh của đa giác. Vì hai cạnh kề cắt nhau tại 1 đỉnh, mà đa giác có n đỉnh, nên có n cách chọn hai cạnh kề tùng với cạnh của đa giác.
Chọn 1 đỉnh còn lại trong n-5 đỉnh (bỏ 3 đỉnh tạo nên hai cạnh kề và 2 đỉnh hai bên). Do đó trường hợp này có n(n-5) tứ giác.
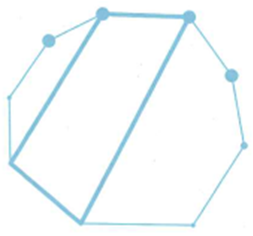
Trường hợp 2: Tứ giác có hai cạnh đối thuộc cạnh của đa giác. Chọn 1 cạnh trong n cạnh của đa giác nên có n cách.
Trong n-4 đỉnh còn lại (bỏ 2 đỉnh tạo nên cạnh đã chọn ở trên và 2 đỉnh liền kề cạnh đã chọn sẽ tạo nên n-5 cạnh.
Chọn 1 cạnh trong n-5 cạnh đó nên có n-5 cách.
Song trường hợp này số tứ giác ta đếm 2 lần, do đó trường hợp này có tứ giác.
Vậy có tất cả: tứ giác.
Áp dụng vào bài với n=20, suy ra .
Suy ra xác suất cần tìm là: .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
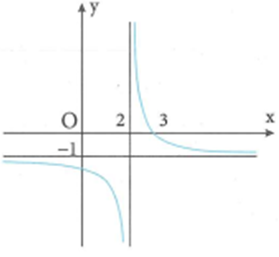
Cho hàm số có đồ thị như hình vẽ bên. Giá trị của a+2b+3c bằng bao nhiêu?
Cho hàm số y=f(x) có đồ thị (C), xác định và liên tục trên ℝ thỏa mãn đồng thời các điều kiện ; và f(0)=2. Phương trình tiếp tuyến tại điểm có hoành độ x=1 của đồ thị (C) là
Cho f'(x)=2x+1 và f(1)=5. Phương trình f(x)=5 có hai nghiệm . Tính tổng .
Có bao nhiêu cách xếp 6 quyển ách lên kệ sách thành một dãy hàng ngang, trong đó có 3 cuốn sách Toán giống nhau và 3 cuốn sách Văn giống nhau?
Một người đem gửi ngân hàng 10 triệu đồng với thể thức lãi suất kép kì hạn 3 tháng với lãi suất 6% một năm. Sau 2 năm người đó đến rút tiền cả vốn lẫn lãi. Hỏi người đó nhận được tất cả bao nhiêu tiền?
Cho số phức z thỏa mãn là một số thuần ảo. Tập hợp điểm biểu diễn số phức z là một dường tròn có diện tích bằng
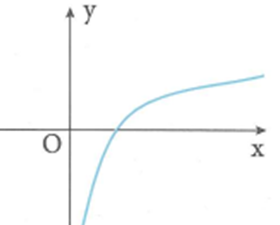
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn hàm số được liệt kê trong các phương án A, B, C, D dưới đây. Tìm f(x)
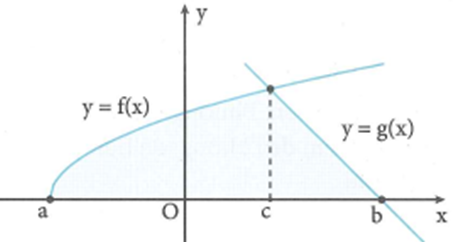
Hình phẳng (H) giới hạn bởi các đồ thị hàm số y=f(x); y=g(x) và trục hoành như hình dưới đây. Thể tích V của khối tròn xoay được tạo ra khi quay (H) quanh trục Ox là
Gọi M là điểm biểu diễn số phức z=1-3i. Khi đó độ dài đoạn OM bằng bao nhiêu?
Cho z là số phức thuần ảo. Trong những khẳng định sau, đâu là khẳng định sai?
Gọi là giá trị lớn nhất làm cho hàm số có giá trị nhỏ nhất trên [1;3] bằng 1. Khi đó gần giá trị nào nhất sau đây?
Gọi lần lượt là thể tích của khối tròn xoay sinh ra bởi một tam giác vuông khi quay quanh cạnh huyền và các cạnh góc vuông của tam giác đó. Biết và . Khi đó giá trị của V là: