Chọn kí hiệu thuộc (∈) hoặc không thuộc (∉) thay cho mỗi ?.
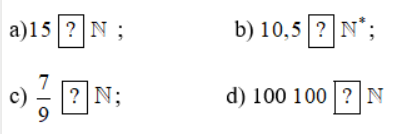
Giải bởi Vietjack
Tập hợp là tập hợp các số tự nhiên: N = {0; 1; 2; 3; 4; 5; …}.
Tập hợp là tập hợp các số tự nhiên khác 0: N* = {1; 2; 3; 4; 5; 6; …}.
Do đó:
a) 15 là số tự nhiên nên 15 thuộc tập hợp N, ta viết 15 ∈ N .
b) Số 10,5 không phải là số tự nhiên nên 10,5 không thuộc tập hợp N*, ta viết 10,5 ∉ N*.
c) Số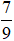 
không phải là số tự nhiên nên 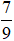không thuộc tập hợp N, ta viết 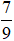∉ N.
d) Số 100 là số tự nhiên nên 100 thuộc tập hợp N nên ta viết 100 ∈ N.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
a) Dựa theo cách biểu diễn trên, hãy biểu diễn các số 345 và 2 021.
b) Đọc số 96 208 984. Số này có mấy chữ số? Số triệu, số trăm là bao nhiêu?
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) 1 999 > 2 003;
b) 100 000 là số tự nhiên lớn nhất;
c) 5 ≤ 5;
d) Số 1 là số tự nhiên nhỏ nhất.
Mỗi số sau có bao nhiêu chữ số? Chỉ ra chữ số hàng đơn vị, hàng chục, hàng trăm, … của mỗi số đó.
2 023; 5 427 198 653.
Thay mỗi chữ cái dưới đây bằng một số tự nhiên phù hợp trong những trường hợp sau:
a) 17, a, b là ba số lẻ liên tiếp tăng dần;
b) m, 101, n, p là bốn số tự nhiên liên tiếp giảm dần.
Biểu diễn các số 1 983; 2 756; 2 053 theo mẫu 1 983 = 1 x 1000 + 9 x 100 + 8 x 10 + 3.
a) Tập hợp N và N* có gì khác nhau?
b) Viết tập hợp sau bằng cách liệt kê các phần tử C = { a ∈ N*| a < 6 }.
Cho tập hợp A gồm các số tự nhiên có tận cùng là số 0 hoặc 5 và nhỏ hơn 36. Liệt kê các phần tử của A theo thứ tự giảm dần.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
