Có bao nhiêu số có bốn chữ số có dạng $\overline{abc\text{d}}$ sao cho $a<b<c\le d$.

Cho hàm số y=f(x) có bảng biến thiên như sau

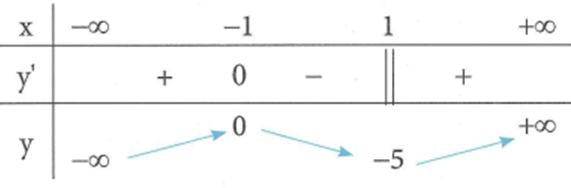
Hàm số có bao nhiêu điểm cực trị?

Tìm nguyên hàm của hàm số f(x)=sin2x.

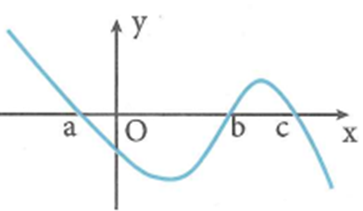
Cho hàm số y=f(x) xác định trên ℝ. Đồ thị hàm số y=f'(x) cắt trục hoành tại ba điểm có hoành độ a, b, c (a<b<c) như hình bên. Biết f(b)<0, hỏi phương trình f(x)=0 có nhiều nhất bao nhiêu nghiệm?

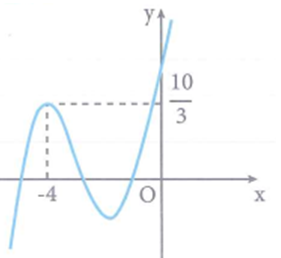
Cho hàm số y=f(x) liên tục và có đạo hàm trên ℝ, có đồ thị như hình vẽ bên. Với m là tham số thực bất kì thuộc đoạn [1;2], phương trình $f(x^3-3{\text{x}}^2)=m^3-3m^2+5$ có bao nhiêu nghiệm thực?

Cho tứ diện đều ABCD cạnh bằng a. Diện tích xung quanh $S_{xq}$ của hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện ABCD là

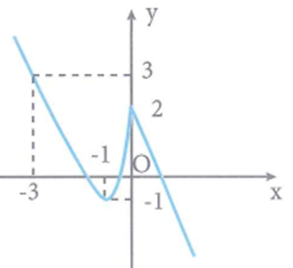
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

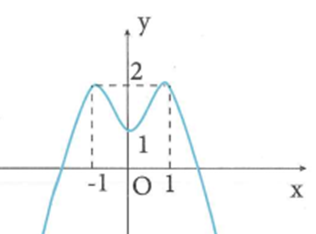
Có bao nhiêu giá trị nguyên của tham số $m\in \left[-100;100\right]$ để phương trình ${\log }_3{x}^{2m+1}=(m+3)(x-1)$ có hai nghiệm thực dương phân biệt?

Cho hàm số y=f(x) liên tục trên ℝ có đồ thị như hình vẽ bên. Xét hàm số $g\left(x\right)=f\left(\frac{x+3}{x-1}\right)+2mg\left(x\right)=f\left(\frac{x+3}{x-1}\right)+2m$. Tìm m để giá trị lớn nhất của g(x) trên đoạn $\left[-1;0\right]$ bằng 1

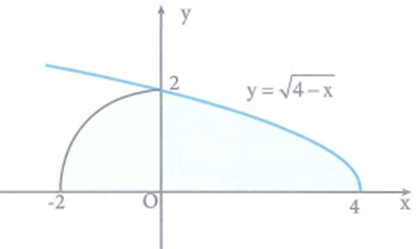
Cho (H) là hình phẳng giới hạn bởi $\frac{1}{4}$ cung tròn có bán kính R = 2, đường cong $y=\sqrt{4-x}$ và trục hoành (miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-3;2), $B(3;5;-2)$. Phương trình mặt phẳng trung trực của AB có dạng $x+ay+b\text{z}+c=0$. Khi đó a+b+c bằng

Cho cấp số nhân $\left(u_n\right)$ có số hạng đầu $u_1=3$ và số hạng thứ tư $u_4=24$. Tính tổng $S_{10}$ của 10 số hạng đầu của cấp số nhân trên

Cho hình lập phương $ABC\text{D}.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Gọi M, N lần lượt là trung điểm các cạnh AD, CD và P là điểm trên cạnh BB' sao cho $BP=3P{B}^{\text{'}}$. Mặt phẳng (MNP) chia khối lập phương thành hai khối lần lượt có thể tích $V_1,{\text{ V}}_2$. Biết khối có thể tích $V_1$ chứa điểm A. Tính tỉ số $\frac{V_1}{V_2}$.

Trong các biểu thức sau, biểu thức nào không có nghĩa?

Gọi a là hệ số không chứa x trong khai triển nhị thức Niu tơn${\left(x^2-\frac{2}{\sqrt{x}}\right)}^n=C_n^0{\left(x^2\right)}^n+C_n^1{\left(x^2\right)}^{n-1}\left(\frac{-2}{\sqrt{x}}\right)+\mathrm{...}+C_n^{n-1}\left(x^2\right){\left(\frac{-2}{\sqrt{x}}\right)}^{n-1}+C_n^n{\left(\frac{-2}{\sqrt{x}}\right)}^n\left(n\in {\mathbb{N}}^{*}\right)$

Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a.

Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây.

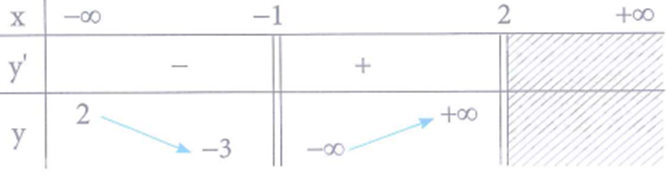
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là