Cho a là số thực và z là nghiệm của phương trình $z^2-2z+a^2-2a+5=0$. Biết $a=a_0$ là giá trị để số phức z có môđun nhỏ nhất. Khi đó $a_0$ gần giá trị nào nhất trong các giá trị sau?

Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có tâm I(3;1;-3) và cắt trục tung Oy tại hai điểm A, B sao cho tam giác IAB vuông. Phương trình mặt cầu (S) là

Hình chữ nhật ABCD có $AB=4,AD=2$. Gọi M và N lần lượt là trung điểm của AB và CD .Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng

Cho hai đường thẳng song song ${\Delta }_1$ và ${\Delta }_2$. Nếu trên hai đường thẳng ${\Delta }_1$ và ${\Delta }_2$ có tất cả 2018 điểm thì số tam giác lớn nhất có thể tạo ra từ 2018 điểm này là

Cho 6 điểm A, B, C, D, E, F cùng thuộc một đường tròn. Hỏi có thể tạo ra được bao nhiêu tam giác có ba đỉnh là ba trong 6 điểm trên?

Gọi M, N là giao điểm của đồ thị $y=\frac{7x+6}{x-2}$ và đường thẳng y=x+2. Khi đó hoành độ trung điểm của đoạn MN bằng

Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{OM}=3\overrightarrow{i}-2\overrightarrow{k}$ với $\overrightarrow{i},\overrightarrow{k}$ lần lượt là vectơ đơn vị trên trục Ox, Oz. Tọa độ điểm M là

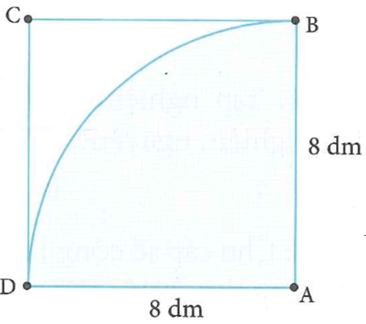
Từ miếng tôn hình vuông ABCD cạnh bằng 8dm, người ta cắt ra hình quạt tâm A bán kính $AB=8\text{dm}$ (như hình vẽ) để cuộn lại thành chiếc phễu hình nón (khi đó AB trùng với AD). Tính thể tích V của khối nón tạo thành

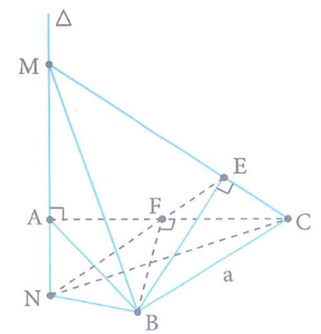
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng $\Delta$ đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E,F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng $\Delta$ cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu?

Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và tam giác ABC. Mệnh đề nào dưới đây đúng?

Tập xác định D của hàm số $y={\log }_x\left(4-x^2\right)$ là

Phương trình 3sinx-1=0 có bao nhiêu nghiệm thuộc khoảng từ $\left(0;3\pi \right)$?

Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số $y=f_1\left(x\right);y=f_2\left(x\right)$ (liên tục trên [a;b]) và hai đường thẳng $x=a,x=b\left(a<b\right)$. Khi đó S được tính theo công thức nào sau đây?

Trong không gian với hệ tọa độ Oxyz , cho hình chóp tứ giác đều S.ABCD biết A(1;0;0); $,B\left(5;0;0\right),C\left(5;4;0\right)$ và chiều cao hình chóp bằng 6. Gọi I(a;b;c) là điểm cách đều 5 đỉnh của hình chóp (với c>0). Tính giá trị của T=a+2b+3c

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, biết SA vuông góc với đáy (ABCD) và SA = 2a. tính khoảng cách h giữa hai đường thẳng AC và SB

Trong tất cả các giá trị của m để đồ thị hàm số $y=\frac{x-4}{\sqrt{m{x}^2+m^2-17}}$ có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên?