Bộ 30 đề thi thử THPT Quốc gia môn Toán năm 2022 có đáp án (Đề số 17)
-
20331 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho số phức z=a+bi với . Môđun của z tính bằng công thức nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Câu 2:
Hàm số nào sau đây có bảng biến thiên như hình bên?
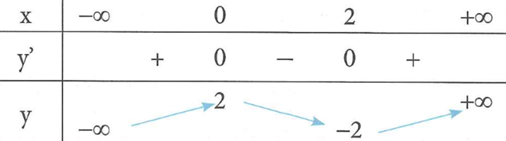
 Xem đáp án
Xem đáp án
Đáp án D
Do loại A, B
Do đồ thị đi qua điểm M(2;-2) nên ta chọn D
Câu 3:
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có bán kính R=2 và tâm O có phương trình
 Xem đáp án
Xem đáp án
Đáp án C
Mặt cầu (S) có bán kính R=2 và tâm O(0;0;0) có phương trình:
Câu 5:
Hàm số có đồ thị (T) là một trong bốn hình dưới đây
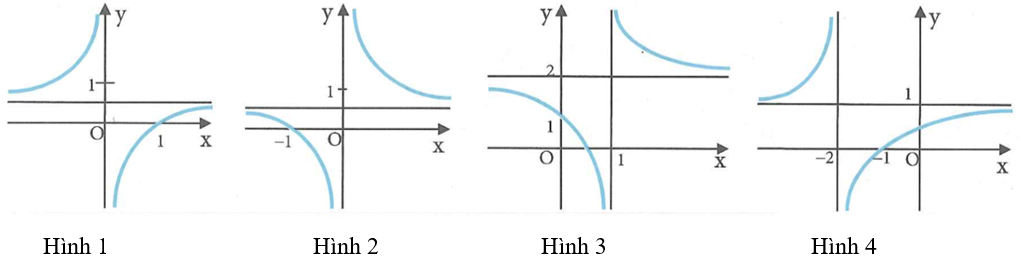
Hỏi đồ thị (T) là hình nào?
 Xem đáp án
Xem đáp án
Đáp án B
Đồ thị nhận x = 0 (trục tung) làm tiệm cận đứng loại C, D
Ta có: nên hàm số nghịch biến trên khoảng và
Câu 6:
Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số (liên tục trên [a;b]) và hai đường thẳng . Khi đó S được tính theo công thức nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án C
Công thức là
Công thức chỉ đúng khi trên [a;b] phương trình vô nghiệm hoặc có nghiệm thì đó là nghiệm kép hoặc nghiệm bội chẵn. Hay trên đoạn [a;b] hai đồ thị và không có giao điểm hoặc tiếp xúc nhau.
Câu 7:
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và tam giác ABC. Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án D
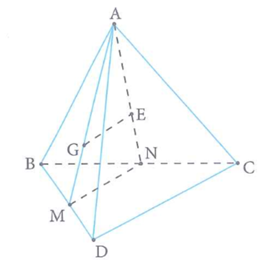
Gọi M, N lần lượt là trung điểm của BD, BC.
Khi đó: (1)
Mặt khác: MN là đường trung bình của
(2)
Từ (1) và (2), suy ra: GE//CD
Câu 8:
Cho hai hàm số và với . Khẳng định nào sau đây sai ?
 Xem đáp án
Xem đáp án
Đáp án D
Đồ thị cắt trục hoành tại điểm M(1;0) nên D sai
Câu 9:
Một hình nón có bán kính đáy bằng 5a, độ dài đường sinh bằng 13a. Tính độ dài đường cao h của hình nón
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Câu 10:
Trong không gian với hệ tọa độ Oxyz, cho với lần lượt là vectơ đơn vị trên trục Ox, Oz. Tọa độ điểm M là
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Nếu
Câu 11:
Một khối tứ diện đều cạnh a có thể tích bằng
 Xem đáp án
Xem đáp án
Đáp án C
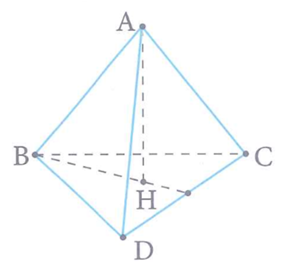
Ta có:
Khi đó:
+) Một tam giác đều cạnh a có:
+) Một khối tứ diện đều cạnh a có:
Câu 12:
Trong các phát biểu sau khi nói về hàm số , phát biểu nào đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có: . Khi đó:
Lập bẳng biến thiên suy ra hàm số có một điểm cực đại x=0 và hai điểm cực tiểu
Với hàm trùng phương để suy luận ra số cực trị (cực đại, cực tiểu) ta chỉ cần dựa vào dấu của hệ số a,b. Cụ thể:
- : Có một cực trị
Một cực đại và không có cực tiểu
Một cực tiểu và không có cực đại
- ab<0: có ba cực trị
Có hai cực đại và một cực tiểu
Có hai cực tiểu và một cực đại
Ở câu hỏi này ta có: hàm số có hai cực tiểu và một cực đại.
Câu 13:
Cho hàm số y=f(x) xác định và liên tục trên , có . Tính tích phân
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Câu 14:
Cho 6 điểm A, B, C, D, E, F cùng thuộc một đường tròn. Hỏi có thể tạo ra được bao nhiêu tam giác có ba đỉnh là ba trong 6 điểm trên?
 Xem đáp án
Xem đáp án
Đáp án A
Số tam giác được tạo thành chính là số cách lấy 3 điểm từ 6 điểm phân biệt không quan tâm tới thứ tự. Do đó số tam giác cần tìm là:
Câu 15:
Có bao nhiêu số nguyên m để phương trình có nghiệm?
 Xem đáp án
Xem đáp án
Đáp án D
Phương trình có nghiệm khi và chỉ khi:
Câu 16:
Cho hình chóp S.ABC trên cạnh SA, SB, SC lần lượt lấy ba điểm A'; B'; C' sao cho và . Gọi V' và V lần lượt là thể tích của khối chóp và S.ABC. Khi đó tỉ số bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Câu 17:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Ở câu hỏi này ta có thể dùng Casio hoặc thay ngược đáp số.
Câu 18:
Cho hàm số có đồ thị (C). Khi đó hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ x=1 là
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Khi đó hệ góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ x=1 là : y'(1)=6
Câu 19:
Biết T(4;-3) là điểm biểu diễn số phức z trên mặt phẳng tọa độ phức Oxy. Khi đó điểm nào sau đây biểu diễn số phức
 Xem đáp án
Xem đáp án
Đáp án D
Do T(4;-3) là điểm biểu diễn số phức z.
Suy ra:
Khi đó điểm Q(1;-3) biểu diễn số phức w.
Câu 20:
Cho 0<m<1 và . Khi đó giá trị nào sau đây gần m nhất?
 Xem đáp án
Xem đáp án
Đáp án B
Đặt . Khi đó:
Suy ra:
gần giá trị 0,69 nhất
Câu 21:
Phương trình 3sinx-1=0 có bao nhiêu nghiệm thuộc khoảng từ ?
 Xem đáp án
Xem đáp án
Đáp án C
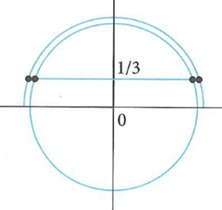
Ta có: (*)
Dựa vào đường tròn lượng giác, suy ra trên khoảng
Phương trình (*) có 4 nghiệm phân biệt
Câu 22:
Gọi M, N là giao điểm của đồ thị và đường thẳng y=x+2. Khi đó hoành độ trung điểm của đoạn MN bằng
 Xem đáp án
Xem đáp án
Đáp án A
Phương trình hoành độ giao điểm:
có 2 nghiệm lần lượt là hoành độ của MN
Khi đó hoành độ trung điểm của đoạn MN là :
Câu 23:
Trong không gian với hệ tọa độ Oxyz, biết M(a;b;c) (với a>0) là điểm thuộc đường thẳng và cách mặt phẳng một khoảng bằng 2. Tính giá trị của T=a+b+c
 Xem đáp án
Xem đáp án
Đáp án D
Do với t=a>0
Khi đó
Câu 24:
Hình chữ nhật ABCD có . Gọi M và N lần lượt là trung điểm của AB và CD .Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
 Xem đáp án
Xem đáp án
Đáp án B
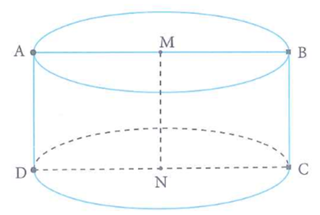
Khối tròn xoay được tạo ra là hình trụ (như hình vẽ)
Ta có
Câu 26:
Biết giá trị lớn nhất của hàm số trên đoạn [-1;1] bằng 0 khi . Hỏi trong các giá trị sau, đâu là giá trị gần nhất?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Ta có:
Vậy gần -1 nhất trong các phương án đưa ra
Câu 27:
Hàm số nghịch biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Xét
Vậy hàm số nghịch biến trên khoảng (-2;0)
Câu 28:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ; và mặt phẳng Oxz cắt lần lượt tại các điểm A, B. Diện tích S của tam giác OAB bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án A
Mặt phẳng Oxz có phương trình: y=0
+) Thay y=0 vào phương trình , suy ra:
+) Thay y=0 vào phương trình , suy ra:
Suy ra
Câu 29:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, biết SA vuông góc với đáy (ABCD) và SA = 2a. tính khoảng cách h giữa hai đường thẳng AC và SB
 Xem đáp án
Xem đáp án
Đáp án B
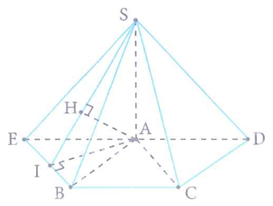
Dựng hình bình hành
(Với I là hình chiếu vuông góc của A trên EB và H là hình chiếu vuông góc của A trên SI như hình vẽ).
Ta có ABE là tam giác vuông cân tại
Khi đó:
Câu 30:
Trong các số phức z thỏa mãn điều kiện . Số phức z có môdun nhỏ nhất có tổng phần thực và hai lần phần ảo là
 Xem đáp án
Xem đáp án
Đáp án B
Cách 1: Gọi z=a+bi với . Khi đó điều kiện bài toán tương đương:
Suy ra:
Vậy khi
Cách 2: Gọi M là điểm biểu diễn số phức z , khi đó:
Trong đó
Suy ra M thuộc đường thẳng trung trực của AB với
Ta có: là hình chiếu vuông góc của O trên đường thẳng
Đường thẳng qua O vuông góc với là: x-y=0
Khi đó tọa độ điểm M là nghiệm của hệ:
đáp số: 2+2.2=6
Câu 31:
Tập nghiệm S của bất phương trình có bao nhiêu nghiệm nguyên?
 Xem đáp án
Xem đáp án
Đáp án C
Phương trình tương đương . Điều kiện:
Đặt với t>0 khi đó phương trình có dạng:
Vậy:
Câu 32:
Cho cấp số cộng có công sai d=-4 và đạt giá trị nhỏ nhất. Tìm là số hạng thứ 2019 của cấp số cộng đó
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
Suy ra: khi
Câu 33:
Trong tất cả các giá trị của m để đồ thị hàm số có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên?
 Xem đáp án
Xem đáp án
Đáp án C
Theo yêu cầu bài toán thì đồ thị phải có 2 tiệm cận đứng và 2 tiệm cận ngang
+) Đồ thị có 2 tiệm cận ngang thì khi .
Nghĩa là đồ thị có 2 tiêm cận ngang
+) Đồ thị có 2 tiệm cận đứng khi và chỉ khi phương trình có 2 nghiệm phân biệt khác 4
Câu 34:
Cho số phức z có môđun bằng 2. Biết rằng tập hợp điểm trong mặt phẳng tạo độ biểu diễn số phức là đường tròn tâm I(a;b), bán kính R. Tổng bằng
 Xem đáp án
Xem đáp án
Đáp án D
Gọi M(x;y) là điểm biểu diễn số phức w=x+yi. Khi đó:
Suy ra M thuộc đường tròn tâm I(4;-3) và bán kính
Câu 35:
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có tâm I(3;1;-3) và cắt trục tung Oy tại hai điểm A, B sao cho tam giác IAB vuông. Phương trình mặt cầu (S) là
 Xem đáp án
Xem đáp án
Đáp án C
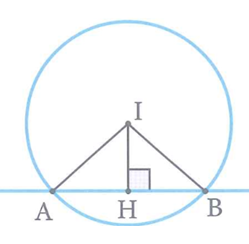
Gọi H là hình chiếu vuông góc của I trên trục Oy
Do IAB là tam giác vuông cân nên suy ra:
Suy ra phương trình mặt cầu
Câu 36:
Cho hàm số y=f(x) liên tục trên đoạn [-3;10], biết và có bảng biến thiên như hình bên:
![Cho hàm số y=f(x) liên tục trên đoạn [-3;10], biết (ảnh 1)](https://hamchoi.vn/storage/uploads/images/3/capture-1638179951.png)
Có bao nhiêu giá trị của m để phương trình có ba nghiệm thực phân biệt thuộc đoạn [-3;10]?
 Xem đáp án
Xem đáp án
Đáp án C
Số nghiệm của phương trình (*) chính là số giao điểm của đồ thị y=f(x) và đường thẳng y=f(m) có phương song song hoặc trùng với trục Ox.
![Cho hàm số y=f(x) liên tục trên đoạn [-3;10], biết (ảnh 2)](https://hamchoi.vn/storage/uploads/images/3/capture-1638180034.png)
Do đó dựa vào bẳng biến thiên của hàm số y=f(x), phương trình (*) có ba nghiệm thực phân biệt (2*)
Từ bảng biến thiên của hàm số y=f(x), ta có:
Khi đó (2*) : có 8 giá trị m
Câu 37:
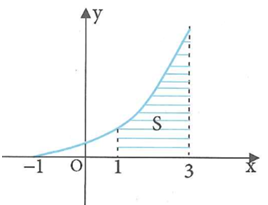
Cho hàm số y=f(x) liên tục trên và hàm số có đồ thị trên đoạn [-1;3] như hình vẽ. Biết miền hình phẳng được tô sọc kẻ có diện tích S=6.
Tính tích phân
 Xem đáp án
Xem đáp án
Đáp án D
Hình phẳng được giới hạn bởi các đường:
Khi đó ta có:
Đặt
Suy ra:
Câu 38:
Gieo một con súc sắc cân đối, đồng chất liên tiếp hai lần. Biết tổng số chấm sau hai lần gieo là m. Tính xác suất để sau hai lần gieo phương trình có nghiệm
 Xem đáp án
Xem đáp án
Đáp án A
Số khả năng xảy ra khi gieo 2 con súc sắc liên tiếp là:
Gọi A là biến cố để phương trình có nghiệm
Với m là tổng số chấm sau 2 lần gieo, suy ra:
Điều kiện để phương trình có nghiệm là:
Trường hợp 1: có 3 cách
Trường hợp 2: có 2 cách
Trường hợp 3: có 1 cách
Suy ra
Câu 39:
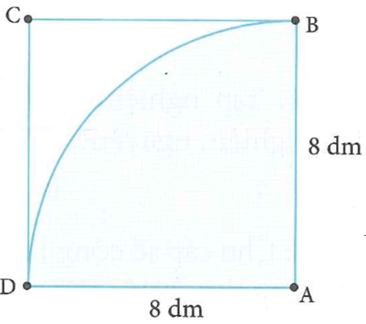
Từ miếng tôn hình vuông ABCD cạnh bằng 8dm, người ta cắt ra hình quạt tâm A bán kính (như hình vẽ) để cuộn lại thành chiếc phễu hình nón (khi đó AB trùng với AD). Tính thể tích V của khối nón tạo thành
 Xem đáp án
Xem đáp án
Đáp án B
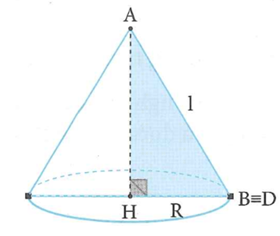
Độ dài cung tròn BD bằng chu vi đường tròn, bán kính AB và bằng chu vi đáy của hình nón.
Do đó ta có:
Suy ra thể tích của nón:
Câu 40:
Trong không gian với hệ tọa độ Oxyz , cho hình chóp tứ giác đều S.ABCD biết A(1;0;0); và chiều cao hình chóp bằng 6. Gọi I(a;b;c) là điểm cách đều 5 đỉnh của hình chóp (với c>0). Tính giá trị của T=a+2b+3c
 Xem đáp án
Xem đáp án
Đáp án B
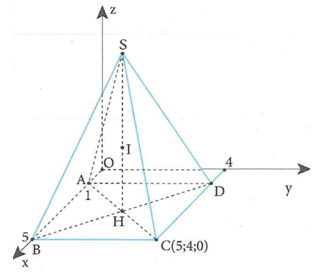
Gọi H là hình chiếu vuông góc của S trên mặt phẳng . Do S.ABCD là chóp đều nên H là giao điểm của AC và (với H là trung điểm của AC)
Theo đề ra ta có:
Vì I cách đều 5 đỉnh của chóp nên suy ra:
. Do
Mặt khác:
Câu 41:
Có tất cả bao nhiêu số nguyên m để phương trình có ba nghiệm thực phân biệt?
 Xem đáp án
Xem đáp án
Đáp án B
Điều kiện: x > 0
Biến đổi phương trình tương đương:
Đặt , khi đó phương trình có dạng:
với là hàm số đồng biến
với x>0
Ta có:
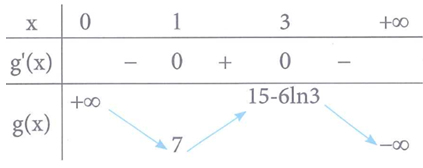
Dựa vào bảng biến thiên, suy ra phương trình có 3 nghiệm khi và chỉ khi:
Câu 42:
Trong không gian với hệ tọa độ Oxyz , cho (P) là mặt phẳng chứa đường thẳng và tiếp xúc với mặt cầu . Khi đó mặt phẳng (P) đi qua điểm nào trong các điểm sau?
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Do , suy ra mặt phẳng (P) có dạng:
với
Mặt cầu (S) có tâm I(1;0;0) và bán kính R=2
Do tiếp (P) xúc với (S) nên:
Chọn đi qua điểm Q(-1;2;0)
Mặt phẳng chứa đường thẳng luôn có dạng:
với
Câu 43:
Cho hàm số y=f(x) liên tục trên có đồ thị y=f'(x) như hình vẽ bên. Hàm số có bao nhiêu điểm cực tiểu?
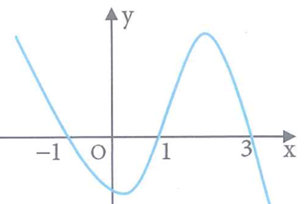
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Khi đó:
Do
(2*)
Từ (*), (2*), suy ra:
Vậy
Tính (do )
Khí đó ta có bẳng xét dấu của y' như sau:
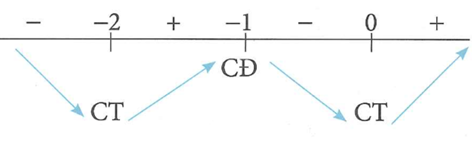
Suy ra hàm số có 2 điểm cực tiểu
Câu 44:
Diện tích hình phẳng giới hạn bởi các đường và parabol bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Tính
 Xem đáp án
Xem đáp án
Đáp án A
Ta có: y'=2ax+b
Do I (1;2) là điểm cực tiểu của
Khi đó (P) có dạng:
Do (P) có đỉnh I(1;2) nằm phía trên trục
Khi đó diện tích hình phẳng
Suy ra:
Câu 45:
Cho hai đường thẳng song song và . Nếu trên hai đường thẳng và có tất cả 2018 điểm thì số tam giác lớn nhất có thể tạo ra từ 2018 điểm này là
 Xem đáp án
Xem đáp án
Đáp án B
Gọi n là số điểm thuộc đường thẳng . Suy ra số điểm thuộc là: 2018-n
+) Nếu n=1, thì số điểm thuộc lần lượt là: 1; 2017. Suy ra số tam giác:
+) Nếu thì tam giác có thể tạo ra thuộc một trong hai trường hợp sau:
Trường hợp 1: Tam giác có 3 đỉnh được lấy từ 1 điểm thuộc và 2 điểm thuộc
Trường hợp 2: Tam giác có 3 đỉnh được lấy từ 2 điểm thuộc và 1 điểm thuộc
Suy ra số tam giác là:
Dấu “=” xảy ra khi n=1009, suy ra :
Câu 46:
Cho a là số thực và z là nghiệm của phương trình . Biết là giá trị để số phức z có môđun nhỏ nhất. Khi đó gần giá trị nào nhất trong các giá trị sau?
 Xem đáp án
Xem đáp án
Đáp án D
Gọi z=x+yi với . Khi đó phương trình có dạng:
. Từ
+) Với , khi đó (*) có dạng:
(vô nghiệm)
+) Với x=1, khi đó (*) có dạng:
Suy ra:
Vậy khi gần 2 nhất (trong các phương án đưa ra)
Câu 47:
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E,F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu?
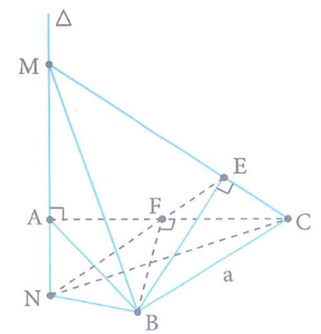
 Xem đáp án
Xem đáp án
Đáp án D
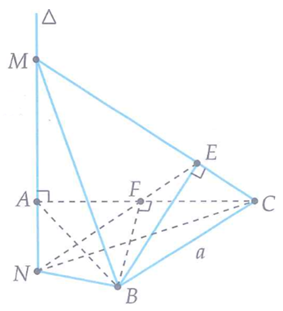
Ta có:
Đặt
Ta có:
Suy ra:
Khi đó:
Suy ra:
Câu 48:
Cho hàm số , với . Biết trên khoảng hàm số đạt giá trị lớn nhất tại x=-1. Vậy trên đoạn hàm số đạt giá trị nhỏ nhất tại
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Vì là điểm cực đại của hàm số
Suy ra:
Khi đó:
Do x=-1 là điểm cực đại nên a > 0, do đó ta có trục dấu của y'(x)
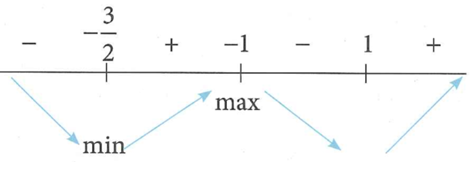
Suy ra hay trên đoạn hàm số đạt giá trị nhỏ nhất tại
Câu 49:
Trong không gian với hệ tọa độ Oxyz, cho phương trình của mặt cầu . Biết với mọi số thực m thì luôn chứa một đường tròn cố định. Tìm bán kíTrong không gian với hệ tọa độ Oxyz, cho phương trình của mặt nh r của đường tròn đó
 Xem đáp án
Xem đáp án
Đáp án B
Gọi M(x;y;z) là điểm cố định là luôn đi qua. Suy ra:
Suy ra tập hợp điểm M là một đường tròn cố định được tạo ra bởi giao điểm của mặt phẳng và mặt cầu
Mặt cầu (S) có tâm I(-1;0;0) và bán kính R=2 và
Suy ra bán kính của đường tròn là:
Câu 50:
Cho phương trình . Hỏi có tất cả bao nhiêu giá trị nguyên của để phương trình trên có nghiệm thực?
 Xem đáp án
Xem đáp án
Đáp án A
Nếu m=0 phương trình có dạng (vô nghiệm)
Nếu thì vế trái của phương trình là đa thức bậc lẻ, vế phải bằng 0. Nên phương trình luôn có nghiệm. Thật vậy:
Đặt khi đó và f(x) liên tục trên
Nên suy ra đồ thị y=f(x) luôn cắt trục Ox , hay phương trình f(x)=0 luôn có nghiệm
Khi đó có 200 số m thỏa mãn
Nếu y=f(x) là một đa thức bậc lẻ thì phương trình f(x)=0 luôn có nghiệm.
