Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;20] để đồ thị hàm số $y=f\left(x^2-2x+m\right)-m$ có 5 đường tiệm cận?

Đường thẳng y=x+1 cắt đồ thị hàm số $y=\frac{2x-1}{x-1}$ tại hai điểm M, N. Độ dài đoạn thẳng MN bằng

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overrightarrow{a}=\left(2;1;-2\right)$ và vectơ $\overrightarrow{b}=\left(1;0;2\right)$. Tìm tọa độ vectơ $\overrightarrow{c}$ là tích có hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$

Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-20;10] để đồ thị hàm số $y=\frac{x+2}{\sqrt{x^2-4x+m}}$ có hai đường tiệm cận đứng?

Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới.

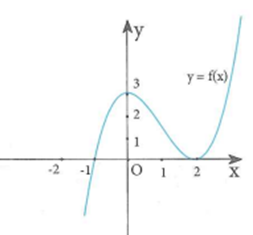
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-2020;2020) để hàm số $y=f\left(\cos x+2x+m\right)$ đồng biến trên nửa khoảng $\left[0;+\infty \right)$.

Tìm nguyên hàm $F\left(x\right)=\int {\sin }^{2}2xdx$

Cho các hàm số $y={\log }_{a}x,y=b^x,y=c^x$ có đồ thị như hình bên. Chọn khẳng định đúng.

Khối chóp S.ABC có SA vuông góc với đáy, SBC là tam giác đều cạnh a, tam giác ABC vuông tại A. Thể tích của khối chóp S.ABC bằng

Cho hàm số y=f(x). Đồ thị y=f'(x) như hình bên.

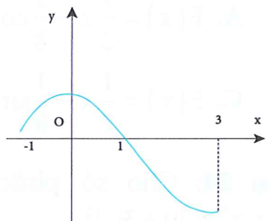
Biết $f\left(-1\right)+f\left(0\right)-2f\left(1\right)=f\left(3\right)-f\left(2\right)$. Giá trị nhỏ nhất của hàm số trên đoạn [-1;3] là

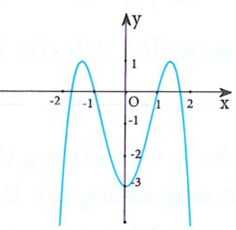
Cho hàm số $y=a{x}^4+b{x}^2+c$ có đồ thị như hình vẽ bên.

Mệnh đề nào dưới đây đúng?

Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi M là trung điểm của AA'. Gọi góc giữa đường thẳng MB' và mặt phẳng $\left(BC{C}^{\text{'}}{B}^{\text{'}}\right)$ là $\alpha$, góc $\alpha$ thỏa mãn đẳng thức nào dưới đây?

Cho hàm số y=sinx+2. Tìm giá trị cực đại của hàm số trên đoạn $\left[-\pi ;\pi \right]$

Cho tam giác ABC đều cạnh a. Quay tam giác ABC quanh đường cao AH ta được hình nón tròn xoay. Diện tích mặt cầu nội tiếp hình nón bằng

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $\left[-2018;2018\right]$ để phương trình ${\left(x+2-\sqrt{x^2+1}\right)}^2+\frac{18\left(x^2+1\right)\sqrt{x^2+1}}{x+2+\sqrt{x^2+1}}=m\left(x^2+1\right)$ có nghiệm thực?

Với a là số thực dương tùy ý khác 1 và b là số thực tùy ý, mệnh đề nào dưới đây đúng?

Cho a, b, c là các số thực thuộc khoảng (0;1), với $a^x=bc,b^y=ca,c^z=ab$. Tìm giá trị nhỏ nhất của biểu thức P=x+y+9z