Cho phương trình: \[{4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\frac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\] với m là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là:
A.4
B.1
C.2
D.3
Giải bởi Vietjack
Ta có:
\[{4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\frac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\]
\[ \Leftrightarrow {2^{ - 2|x - m|}}.2.lo{g_2}({x^2} - 2x + 3) - {2^{2x - {x^2}}}.lo{g_2}(2|x - m| + 2) = 0\]
\[ \Leftrightarrow {2^{ - 2|x - m| + 1}}.lo{g_2}({x^2} - 2x + 3) = {2^{2x - {x^2}}}.lo{g_2}(2|x - m| + 2)\]
\[ \Leftrightarrow {2^{{x^2} - 2x}}.lo{g_2}({x^2} - 2x + 3) = {2^{2|x - m| - 1}}.lo{g_2}(2|x - m| + 2)\]
\[ \Leftrightarrow {2^{{x^2} - 2x}} + 2.lo{g_2}({x^2} - 2x + 3) = {2^{2|x - m| + 2}}.lo{g_2}(2|x - m| + 2)\]
Xét hàm đặc trưng\[f\left( t \right) = {2^t}.{\log _2}t\,\,\left( {t \ge 2} \right)\] ta có
\[f'\left( t \right) = {2^t}.\ln 2.{\log _2}t + {2^t}.\frac{1}{{t\ln 2}} > 0\,\,\forall t \ge 2\] do đó hàm số đồng biến trên\[\left[ {2; + \infty } \right)\]
Lại có\[f\left( {{x^2} - 2x + 3} \right) = f\left( {2\left| {x - m} \right| + 2} \right)\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow {x^2} - 2x + 3 = 2\left| {x - m} \right| + 2}\\{ \Leftrightarrow {x^2} - 2x + 1 = 2\left| {x - m} \right|}\\{ \Leftrightarrow {{\left( {x - 1} \right)}^2} = 2\left| {x - m} \right|\,\,\left( * \right)}\end{array}\]
Để phương trình ban đầu có 3 nghiệm phân biệt thì phương trình (*) phải có 3 nghiệm phân biệt.
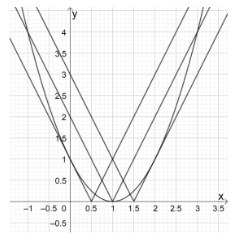
Dựa vào đồ thị hàm số ta có \[m = \frac{1}{2},\,\,m = 1,\,\,m = \frac{3}{2}\] thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Giải phương trình \[{\log _3}\left( {x + 2} \right) + {\log _9}{\left( {x + 2} \right)^2} = \frac{5}{4}\]
Cho các số thực dương a,b,c khác 1 thỏa mãn
Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \[P = lo{g_a}ab - lo{g_b}bc\]. Tính giá trị của biểu thức \[S = 2{m^2} + 9{M^2}\].
Cho phương trình \[{11^x} + m = {\log _{11}}\left( {x - m} \right)\]với mm là tham số. Có bao nhiêu giá trị nguyên của \[m \in \left( { - 205;205} \right)\] để phương trình đã cho có nghiệm?
Giải phương trình \[{\log _3}\left( {2x - 1} \right) = 2\] , ta có nghiệm là:
Giải phương trình \[{\log _2}\left( {{2^x} - 1} \right).{\log _4}\left( {{2^{x + 1}} - 2} \right) = 1\] Ta có nghiệm:
Giải phương trình: \[\mathop \smallint \limits_0^2 \left( {t - {{\log }_2}x} \right)dt = 2{\log _2}\frac{2}{x}\] (ẩn x)
Tìm tập nghiệm S của phương trình \[lo{g_2}({x^2} - 4x + 3) = lo{g_2}(4x - 4)\]
Tìm tập nghiệm S của phương trình \[{\log _2}\left( {x - 1} \right) + {\log _2}\left( {x + 1} \right) = 3\].
Tập nghiệm của phương trình \[{\log _2}\left( {{x^2} - 1} \right) = {\log _2}2x\] là:
Phương trình \[{\log _4}\left( {{{3.2}^x} - 1} \right) = x - 1\] có hai nghiệm là \[{x_1};{x_2}\;\] thì tổng \[{x_1} + {x_2}\;\] là:
Hỏi có bao nhiêu giá trị m nguyên trong đoạn \[\left[ { - 2017;2017} \right]\;\]để phương trình \[logmx = 2log(x + 1)\;\;\] có nghiệm duy nhất?
Cho x,y là các số thực dương thỏa mãn \[lo{g_2}\frac{{3x + 3y + 4}}{{{x^2} + {y^2}}} = (x + y - 1)(2x + 2y - 1) - 4\left( {xy + 1} \right)\] Giá trị lớn nhất của biểu thức \[P = \frac{{5x + 3y - 2}}{{2x + y + 1}}\;\] bằng:
Tìm m để phương trình \[mln(1 - x) - lnx = m\] có nghiệm \[x \in \left( {0;1} \right)\]
