Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A′B′C′ có \[A\prime (\sqrt 3 ; - 1;1),\] hai đỉnh B,C thuộc trục Oz và AA′=1 (C không trùng với O). Biết véc tơ \[\overrightarrow u = \left( {a;b;2} \right)\;\]với \[a,b \in R\mathbb{R}\] là một véc tơ chỉ phương của đường thẳng A′C. Tính \[T = {a^2} + {b^2}\].
A.T=5
B.T=16
C.T=4
D.T=9
Giải bởi Vietjack
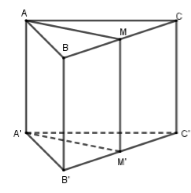
Phương trình \[BC \equiv Oz:\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 0}\\{z = t}\end{array}} \right.\]
Mặt phẳng\[\left( {AMM'A'} \right)\] đi qua A′ và vuông góc với BC nên\[\left( {AMM'A'} \right)\] đi qua\[A'\left( {\sqrt 3 ; - 1;1} \right)\] và nhận\[\vec k = \left( {0;0;1} \right)\] làm VTPT hay
\[\left( {AMM'A'} \right):0\left( {x - \sqrt 3 } \right) + 0\left( {y + 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow z = 1\]
\[M = BC \cap \left( {AMM'A'} \right) \Rightarrow t - 1 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {0;0;1} \right)\]
Mà \[AA' = 1,A'M = \sqrt {{{\left( {\sqrt 3 - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2} + {{\left( {1 - 1} \right)}^2}} = 2\]
\[ \Rightarrow AM = \sqrt {A'{M^2} - A'{A^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \]
Tam giác ABC đều có độ dài đường cao\[AM = \frac{{BC\sqrt 3 }}{2} = \sqrt 3 \Rightarrow BC = 2\]
Gọi \[B\left( {0;0;m} \right),C\left( {0;0;n} \right)\] với\[n \ne 0\] thì \[BC = 2 \Leftrightarrow \left| {m - n} \right| = 2\] và M(0;0;1) là trung điểm \[BC \Leftrightarrow \frac{{m + n}}{2} = 1 \Leftrightarrow m + n = 2\]
Khi đó \[m = 0,n = 2\] vì\[n \ne 0\] hay C(0;0;2).
\[ \Rightarrow \overrightarrow {A'C} = \left( { - \sqrt 3 ;1;1} \right)\] hay\[2\overrightarrow {AC'} = \left( { - 2\sqrt 3 ;2;2} \right)\] là một VTCP của A′CA′C.
Suy ra \[a = - 2\sqrt 3 ,b = 2 \Rightarrow {a^2} + {b^2} = {\left( { - 2\sqrt 3 } \right)^2} + {2^2} = 16\]
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz, gọi M′ là điểm đối xứng của điểm M(2;0;1) qua đường thẳng \[\Delta :\frac{x}{1} = \frac{{y + 2}}{2} = \frac{{z - 1}}{1}\]. Tính khoảng cách từ điểm M′ đến mặt phẳng (Oxy).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x−2y−z+7=0 và điểm A(1;1;−2). Điểm H(a;b;c) là hình chiếu vuông góc của A trên (P). Tổng a+b+c bằng:
Đề thi THPT QG - 2021 - mã 101
Trong không gian Oxyz, cho điểm M(−1;3;2) và mặt phẳng (P):x−2y+4z+1=0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+2y−3z+4=0 và đường thẳng\[d:\frac{{x + 2}}{1} = \frac{{y - 2}}{1} = \frac{z}{{ - 1}}.\]Đường thẳng Δ nằm trong (P) đồng thời cắt và vuông góc với d có phương trình:
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(4;−3;5) và B(2;−5;1).Viết phương trình mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng \[\left( d \right):\frac{{x + 1}}{3} = \frac{{y - 5}}{{ - 2}} = \frac{{z + 9}}{{13}}\].
Trong không gian với hệ tọa độ Oxyz, điểm A′(a;b;c) đối xứng với điểm A(−1;0;3) qua mặt phẳng (P):x+3y−2z−7=0. Tìm a+b+c
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (P) đi qua hai điểm A(1;1;2),B(0;−1;1) và song song với đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y + 1}}{{ - 1}} = \frac{z}{2}\;\] là:
Cho \[d:\frac{{x + 1}}{2} = \frac{{y - 3}}{m} = \frac{{z - 1}}{{m - 2}};\,\,\,(P):x + 3y + 2z - 5 = 0\]. Tìm m để d và (P) vuông góc với nhau.
Trong không gian Oxyz, cho hai điểm A(2;−2;4);B(−3;3;−1) và mặt phẳng (P):2x−y+2z−8=0. Xét điểm M là điểm thay đổi thuộc (P), giá trị nhỏ nhất của \[2M{A^2} + 3M{B^2}\;\]bằng:
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD có các đỉnh A(1;2;1),B(−2;1;3),C(2;−1;1),D(0;3;1). Phương trình mặt phẳng (P) đi qua hai điểm A,B sao cho C,D cùng phía so với (P) và khoảng cách từ C đến (P) bằng khoảng cách từ D đến (P) là:
Cho đường thẳng d có phương trình \(d:\left\{ {\begin{array}{*{20}{c}}{x = 2t}\\{y = 1 - t}\\{z = 3 + t}\end{array}} \right.\) và mặt phẳng (P) có phương trình \[(P):x + y + z - 10 = 0\]. Trong các khẳng định sau, khẳng định nào đúng?
Cho đường thẳng \[d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 2}} = \frac{z}{3}\] và mặt phẳng \[\left( P \right):x + y - z - 3 = 0\]. Tọa độ giao điểm của d và (P) là:
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng \[(\alpha ):4x + 3y - 7z + 1 = 0\]. Phương trình tham số của d là:
Trong không gian với hệ tọa độ Oxyz, cho cho mặt phẳng (P):x−2y+3z−1=0 và đường thẳng \[d:\frac{{x - 1}}{3} = \frac{{y - 2}}{3} = \frac{{z - 3}}{1}\]. Khẳng định nào sau đây đúng:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 2 - 2t}\\{y = 0}\\{z = t}\end{array}} \right.\). Gọi d′ là đường thẳng đối xứng với d qua mặt phẳng (Oxy). Biết phương trình đó có dạng: \(d':\left\{ {\begin{array}{*{20}{c}}{x = a + bt}\\{y = c}\\{z = t}\end{array}} \right.\)
Tính a+b+c.
