 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
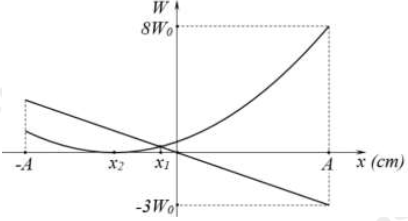
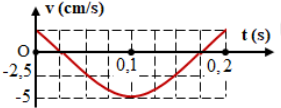
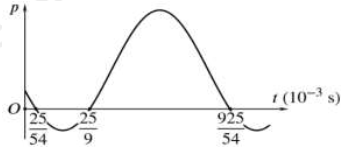
+ Đọc đồ thị
+ Sử dụng biểu thức: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)
+ Sử dụng biểu thức: \(\frac{{CU_0^2}}{2} = \frac{{LI_0^2}}{2}\)
Cách giải:
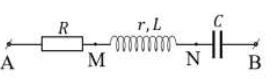
Trong mạch LC ta có: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)
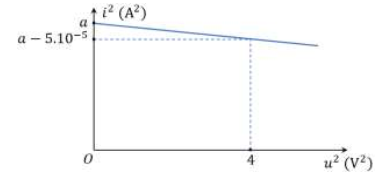
Từ đồ thị, ta có:
+ Tại \({u^2} = 0\) thì \({i^2} = a \Rightarrow I_0^2 = a\)
+ Tại \({u^2} = 4\) thì \({i^2} = a - {5.10^{ - 5}}\) ta suy ra: \(\frac{{a - 5 \cdot {{10}^{ - 5}}}}{{I_0^2}} + \frac{4}{{U_0^2}} = 1 \Leftrightarrow \frac{{a - 5 \cdot {{10}^{ - 5}}}}{a} + \frac{4}{{U_0^2}} = 1 \Rightarrow U_0^2 = 80000{\rm{a}}\)
Lại có:
\(I_0^2 = \frac{C}{L}U_0^2 \Leftrightarrow a = \frac{{{{2.10}^{ - 9}}}}{L} \cdot 80000a \Rightarrow L = {1,6.10^{ - 4}}H = 0,16mH\)
Chọn A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết