Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), tam giác \(SAD\) đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(I\) là điểm thỏa mãn \(\overrightarrow {BI} = \overrightarrow {AC} \). Khoảng cách giữa hai đường thẳng \(SI\) và \(AC\) là
A. \(\frac{{a\sqrt 5 }}{{10}}\).
B. \(\frac{{a\sqrt 5 }}{5}\).
C. \(\frac{{2a\sqrt 5 }}{5}\).
D. \(\frac{{a\sqrt 5 }}{{15}}\).
 Giải bởi Vietjack
Giải bởi Vietjack
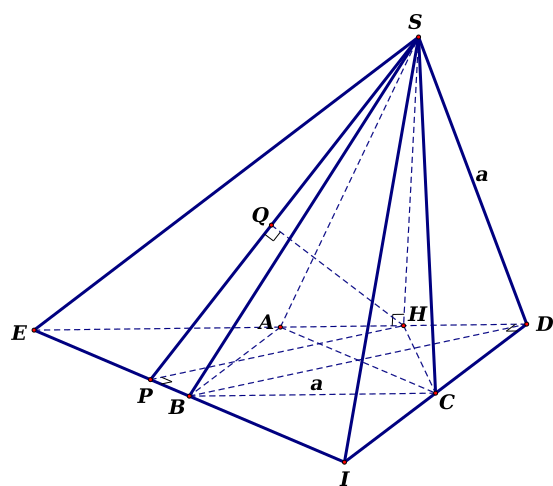
Gọi \(H\) là trung điểm của \(AD\). Vì tam giác \(SAD\) đều cạnh \(a\) nên \(SH \bot AD\)và \(SH = \frac{{a\sqrt 3 }}{2}\). Do tam giác \(SAD\) nằm trong mặt phẳng vuông góc với đáy nên \(SH \bot \left( {ABCD} \right)\).
Vì \(AC//BI\) nên \(AC//\left( {SBI} \right)\) suy ra \(d\left( {AC,SI} \right) = d\left( {AC,\left( {SBI} \right)} \right) = d\left( {A,\left( {SBI} \right)} \right)\).
Gọi \(E\) là giao điểm của \(AD\) và \(BI\). Dễ thấy \(AE = AD\) nên \(\frac{{AE}}{{HE}} = \frac{2}{3}\).
Lại có \(\frac{{d\left( {A,\left( {SBI} \right)} \right)}}{{d\left( {H,\left( {SBI} \right)} \right)}} = \frac{{AE}}{{HE}} = \frac{2}{3}\). Từ đó suy ra \(d\left( {AC,SI} \right) = \frac{2}{3}d\left( {H,\left( {SBI} \right)} \right)\).
Kẻ \(HP \bot BI{\rm{ }}\left( {P \in BI} \right)\), \(HQ \bot SP{\rm{ }}\left( {Q \in SP} \right)\). Khi đó \(d\left( {H,\left( {SBI} \right)} \right) = HQ\).
Ta có \(HP = \frac{3}{4}BD = \frac{{3a\sqrt 2 }}{4}\).
Từ đó ta có \(\frac{1}{{H{Q^2}}} = \frac{1}{{H{P^2}}} + \frac{1}{{S{H^2}}} = \frac{8}{{9{a^2}}} + \frac{4}{{3{a^2}}} = \frac{{20}}{{9{a^2}}} \Rightarrow HQ = \frac{{3a\sqrt 5 }}{{10}}\).
Vậy \(d\left( {AC,SI} \right) = \frac{2}{3}.\frac{{3a\sqrt 5 }}{{10}} = \frac{{a\sqrt 5 }}{5}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Diện tích toàn phần của một hình nón có độ dài đường sinh \[l\] gấp đôi bán kính đáy \[r\] là
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \[AB = 2a,\,\,AD = a,\,\,SA = 3a\] và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\), điểm \(E \in SA\)sao cho \(SE = a\), cosin của góc giữa hai mặt phẳng\(\left( {SAC} \right)\) và \(\left( {BME} \right)\) bằng
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên dưới. Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc \(\left[ {1;2020} \right]\) để hàm số \(g\left( x \right) = f\left( {{x^4} - 2{x^2} + m} \right)\) có đúng \(3\) điểm cực trị. Tổng tất cả các phần tử của \(S\) là?
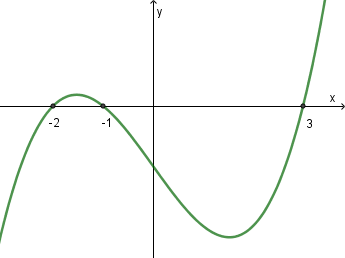
Có bao nhiêu cặp số nguyên dương\(\left( {x;y} \right)\)thỏa mãn:\(2y{.2^x} = {\log _2}\left( {1 + \frac{{2x}}{y}} \right) + 2y + 3x\)
Cho hàm số \(y = \frac{{ax - 2}}{{cx + d}}\) có đồ thị như hình vẽ bên dưới
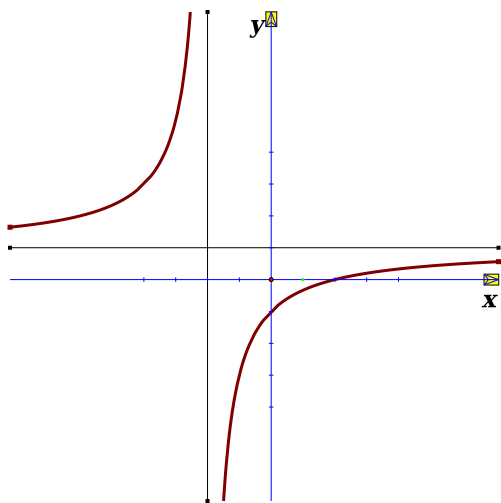
Mệnh đề nào sau đây đúng
Trên giá sách có \[10\] quyển sách tiếng Việt khác nhau, \[8\] quyển sách Toán khác nhau. Hỏi có bao nhiêu cách chọn một quyển sách?
Cho hai hàm số đa thức bậc bốn \(y = f(x)\) và \(y = g(x)\)có đồ thị như hình vẽ, trong đó đường đậm hơnlà đồ thị hàm số \(y = f(x)\). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là \( - 3\) và cắt nhau tại hai điểm nữa có hoành độ lần lượt là \( - 1\) và \(3\). Số giá trị nguyên của tham số \(m \in \left[ { - 12;12} \right]\) để bất phương trình \(f(x) \ge g(x) + m\) nghiệm đúng với mọi \(x \in {\rm{[}} - 3;3]\)?

Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \[\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\] thỏa mãn: \[f\left( {1 + 4\sin x} \right) - \sin x.f\left( {3 - 2\cos 2x} \right) = 6\sin x + 1\] , \[\forall x \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\]. Khi đó \[I = \int\limits_{ - 3}^1 {f\left( x \right)dx} \] bằng:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới.
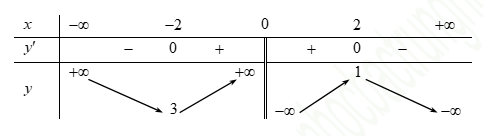
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội \(q = 3\). Tính \({u_3}\).
Cho hàm số \(f(x)\) có \(f\left( 3 \right) = \frac{9}{2}\) và \(f\prime (x) = \frac{{{x^3} + {x^2} - 1}}{{{x^2} + x + \sqrt {x + 1} }}{\rm{ }}\forall x >- 1\). Tính \(\int\limits_0^3 {f\left( x \right)} {\rm{d}}x\) bằng
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị là đường cong trong hình vẽ bên dưới. Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại điểm
![Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị là đường cong trong hình vẽ bên dưới. Hàm số \(y = f\left( x \right)\) đạt cực tiểu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/04/2-1649730077.png)
Cho biết sự rằng tỉ lệ tăng dân số thế giới hàng năm là \(1,32\% \), nếu tỉ lệ tăng dân số không thay đổi thì đến tăng trưởng dân số được tính theo công thức tăng trưởng liên tục \(S = A.{{\rm{e}}^{Nr}}\)trong đó \(A\) là dân số tại thời điểm mốc, \(S\) là số dân sau \(N\) năm, \(r\) là tỉ lệ tăng dân số hàng năm. Năm \(2013\) dân số thể giới vào khoảng \(7095\) triệu người. Biết năm \(2020\) dân số thế giới gần nhất với giá trị nào sau đây?
Xét các số thực dương \(a,\,b\) thỏa mãn \[{\log _9}a = \log {}_{12}b = \log {}_{15}\left( {a + b} \right)\]. Mệnh đề nào dưới đây đúng?
Trong không gian \[Oxyz\], cho mặt cầu \(\left( S \right)\): \({x^2} + {y^2} + {z^2} - 2x - 2y + 6z - 11 = 0\). Tọa độ tâm mặt cầu\(\left( S \right)\,\)là \(I\left( {a\,;\,b\,;\,c} \right)\). Tính \(a + b + c\)?