Cho hình nón có chiều cao \[{\rm{h}} = 20(cm)\], đường tròn đáy có tâm \[O\] bán kính đường tròn đáy \[r = 25(cm)\]. Một thiết diện đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm \[A,B\]sao cho \[AB = 40(cm)\]. Diện tích mặt cầu tâm\[O\] tiếp xúc với thiết diện bằng
A. \[S = 576\pi (c{m^2})\].
B. \[S = 567\pi (c{m^2})\].
C. \[S = 675\pi (c{m^2})\].
D. \[S = 2304\pi (c{m^2})\]
Giải bởi Vietjack
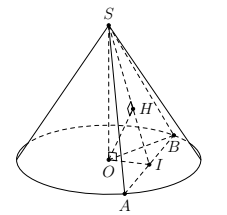Giả sử thiết diện của hình chóp là tam giác \[SAB\], với \[S\] là đỉnh của hình chóp, gọi \[I\] là trung điểm của \[AB\], Gọi \[H\]là hình chiếu vuông góc của \[O\] lên mặt phẳng \[(SAB)\], \[OH\]chính là bán kính mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng thiết diện\[(SAB)\]
Ta có \[AB = 40(cm) \Rightarrow IB = 20(cm)\]
Áp dụng định lí pitago cho tam giác \[OIB\]vuông tại \[I\]
\[OI = \sqrt {O{B^2} - I{B^2}} = \sqrt {{{25}^2} - {{20}^2}} = 15(cm)\]
Xét tam giác \[SOI\] vuông tại \[O\] ta có
\[\frac{1}{{O{H^2}}} = \frac{1}{{{\rm{O}}{{\rm{S}}^2}}} + \frac{1}{{O{I^2}}}\]
\[\frac{1}{{O{H^2}}} = \frac{1}{{{\rm{2}}{{\rm{0}}^2}}} + \frac{1}{{{{15}^2}}} \Rightarrow O{H^2} = 144 \Rightarrow OH = 12(cm)\]
\[S = 4\pi {r^2} = 4.\pi {.12^2} = 576\pi (c{m^2})\]
Chọn đáp án A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian \[Oxyz\] cho tam giác \[ABC\] có \[A(2;\,2;\,0)\], \[B(1;\,0;\,2)\], \[C(0;\,4;\,4)\]. Viết phương trình mặt cầu có tâm là \(A\) và đi qua trọng tâm \[G\] của tam giác \(ABC\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang vuông tại \[A;\;B\]. Gọi \[G\] là trọng tâm tam giác \[SAB\]. Biết \[SA = a\sqrt 6 \] và vuông góc với mặt đáy \[(ABCD)\],\[AB = BC = \frac{1}{2}AD = a\]. Tính theo \[a\] khoảng cách từ \[G\] đến mặt phẳng \[\left( {SCD} \right)\].
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^2 {f\left( x \right)} \,{\rm{d}}x = 9;\int\limits_2^4 {f\left( x \right)\,} {\rm{d}}x = 4\). Tính \(I = \int\limits_0^4 {f\left( x \right)} \,{\rm{d}}x\)?
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y - z = 0\) và mặt phẳng \(\left( Q \right):2x - y + z = 0\). Giao tuyến của mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có phương trình là
Trong không gian \[Oxyz\], cho mặt phẳng\((\alpha ):2x + y - z + 1 = 0\). Vectơ nào sau đây không là vectơ pháp tuyến của mặt phẳng \[(\alpha )\]?
Đường thẳng đi qua điểm \(M\left( {3;2;1} \right)\) và vuông góc với mặt phẳng \(\left( P \right):2x - 5y + 4 = 0\) có phương trình là
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \({u_5} = 10\). Tính tổng \(5\) số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\).
Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Tìm tọa độ điểm biểu diễn số phức \(\frac{{7 - 4i}}{{{z_1}}}\) trên mặt phẳng phức?
Thể tích khối lăng trụ có chiều cao bẳng \(2\) và diện tích đáy bằng \(6\) là
Trong không gian \[Oxyz\], mặt phẳng \[\left( {Oyz} \right)\]có phương trình là
Cho\[x\], \[y\], \[z\] là các số thực khác \[0\]thỏa mãn\[{2^x} = {3^y} = {6^{ - z}}\]. Tính giá trị biểu thức \[M = xy + yz + zx\].
Hỏi có bao nhiêu cách xếp bốn bạn An, Bình, Cường, Dũng ngồi vào một bàn học gồm bốn chỗ?
Tập xác định của hàm số \(y = {\log _5}\left( {2x + 1} \right)\) là
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ.
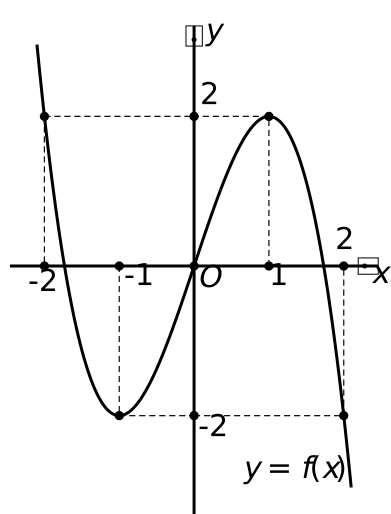
Phương trình \[f\left( {2\cos x} \right) = 2\] có bao nhiêu nghiệm \[x \in \left[ {0;3\pi } \right]\]?
