Theo một thống kê cho thấy, tại một tỉnh X tỉ lệ một người nam giới có người yêu \(P\) tỉ lệ thuận với chiều cao \(h\)(cm) của họ. Người ta xác định được rằng tỉ lệ thoát ế trên được tính bằng công thức \(P(h) = \frac{1}{{1 + 27{e^{ - 0,02h}}}}\). Hỏi một người nam phải cao ít nhất bao nhiêu cm để tỉ lệ họ có người yêu đạt hơn \(50\% \).
A. \(160\).
Giải bởi Vietjack
Chọn đáp án D
Để tỉ lệ người đó có người yêu đạt trên \(50\% \)
\( \Leftrightarrow P(h) >\frac{1}{2} \Leftrightarrow \frac{1}{{1 + 27{e^{ - 0,02h}}}} >\frac{1}{2}\)
\( \Leftrightarrow 1 + 27{e^{ - 0,02h}} < 2 \Leftrightarrow {e^{ - 0,02h}} < \frac{1}{{27}}\)
\( \Leftrightarrow - 0.02h < \ln \frac{1}{{27}} \Leftrightarrow h >\frac{{\ln \frac{1}{{27}}}}{{ - 0.02}} \approx 164.79\).</>
Vậy người đó cần cao ít nhất \(165\)(cm) .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho khối chóp có thể tích \[V = 10\] và chiều cao \[h = 6\]. Diện tích đáy của khối chóp đã cho bằng
Có bao nhiêu cách chia 6 đồ vật khác nhau cho 3 bạn An, Bình , Công sao cho An được 1 đồ vật , Bình được 2 đồ vật và Công được 3 đồ vật.
Diện tích S của hình phẳng giới hạn bởi các đường \(y = 2{x^2} + 3x + 1\,,\,y = {x^3} + 1\,\) được tính bởi công thức nào dưới đây ?
Cho hình chóp \(S.ABCD\) có chiều cao bằng \(12\) và diện tích đáy bằng \(27\). Đáy \(ABCD\) là hình bình hành. Gọi \(M\), \(N\), \(E\), \(F\) lần lượt là trọng tâm các tam giác \(SAB\), \(SBC\), \(SCD\), \(SAD\). Tính thể tích khối đa diện lồi có các đỉnh là các điểm \(M\), \(N\), \(E\), \(F\), \(A\), \(B\), \(C\), \(D\).
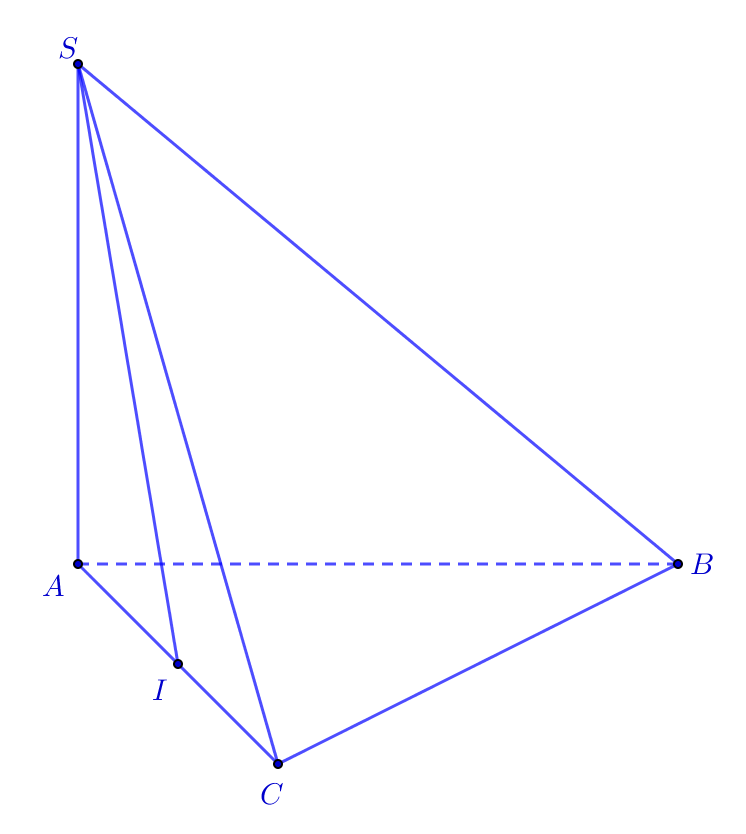
Cho hình chóp \(S.ABCD\) có \[SA\,\]vuông góc với mặt phẳng \(\left( {ABCD} \right)\), \(SA = \frac{{a\sqrt 2 }}{2}\), đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\) có \(AB = 2AD = 2DC = a\) (Hình vẽ minh họa). Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng
Tiệm cận đứng của đồ thị hàm số \[y = \frac{{2x - 2}}{{{x^2} - 1}}\] là
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(4a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = a\sqrt 3 \) (minh họa như hình bên).
Gọi \(I\) là trung điểm của \(AC\). Khoảng cách giữa hai đường thẳng \(SI\) và \(AB\) bằng
Cho cấp số cộng \(({u_n})\)có \({u_1} = 4;\,{u_2} = 1\). Giá trị của \({u_{10}}\)bằng:
Tìm tập xác định \(D\)của hàm số\(y = {\left( {{x^2} - 1} \right)^{\frac{\pi }{3}}}\).
Cho khối lăng trụ có đáy là hình vuông cạnh
\(a\), đường cao bằng \(a\sqrt 2 \)có thể tích bằng:
Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(z = - 1 - 2i\) là điểm nào dưới đây?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(f'\left( x \right) = \left( {2x - 3} \right){\left( {x + 1} \right)^2}{\left( {x - 2} \right)^3}\left( {4 - x} \right)\). Số điểm cực đại của hàm số \(y = f\left( x \right)\) là
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \(A\left( {2; - 3;1} \right)\) trên mặt phẳng \[\left( {Oxy} \right)\]có tọa độ là
