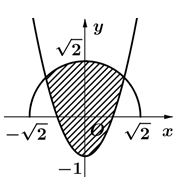
Cho (H) là hình phẳng giới hạn bởi parabol \[y = 2{x^2} - 1\] và nửa đường tròn có phương trình \[y = \sqrt {2 - {x^2}} \] (với \[ - \sqrt 2 \le x \le \sqrt 2 \]) (phần gạch chéo trong hình vẽ). Diện tích của (H) bằng
A.
\[\frac{{3\pi + 2}}{6}.\]
B.\[\frac{{3\pi - 2}}{6}.\]
C.\[\frac{{3\pi + 10}}{6}.\]
D.\[\frac{{3\pi + 10}}{3}.\]
Giải bởi Vietjack
Chọn đáp án C
Phương trình hoành độ giao điểm của hai đồ thị là: \[2{x^2} - 1 = \sqrt {2 - {x^2}} \]
\[ \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 1 \ge 0\\4{x^4} - 4{x^2} + 1 = 2 - {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 1 \ge 0\\4{x^4} - 3{x^2} - 1 = 0\end{array} \right. \Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\].
Diện tích hình \[\left( H \right)\] bằng: \[S = 2\int\limits_0^1 {\left( {\sqrt {2 - {x^2}} - 2{x^2} + 1} \right)dx} = 2\int\limits_0^1 {\sqrt {2 - {x^2}} dx} + 2\int\limits_0^1 {\left( { - 2{x^2} + 1} \right)dx} \]
\[ = 2{I_1} + \left. {2\left( {\frac{{ - 2{x^3}}}{3} + x} \right)} \right|_0^1 = 2{I_1} + \frac{2}{3}\].
Tính \[{I_1} = \int\limits_0^1 {\sqrt {2 - {x^2}} dx} \] đặt \[x = \sqrt 2 \sin t \Rightarrow dx = \sqrt 2 \cos tdt\] với \[t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\]
Đổi cận\[\left| \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = \frac{\pi }{4}\end{array} \right.\]\[ \Rightarrow {I_1} = \int\limits_0^{\frac{\pi }{4}} {\sqrt {2 - 2{{\sin }^2}t} .\sqrt 2 \cos tdt} = \int\limits_0^{\frac{\pi }{4}} {2{{\cos }^2}tdt} = \int\limits_0^{\frac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt} \]
\[ = \left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\frac{\pi }{4}} = \frac{\pi }{4} + \frac{1}{2} \Rightarrow S = 2{I_1} + \frac{2}{3} = \frac{\pi }{2} + 1 + \frac{2}{3} = \frac{{3\pi + 10}}{6}\].
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai số phức \[{z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 - 3i.\] Số phức \[w = {z_1} + {z_2}\] có phần thực bằng
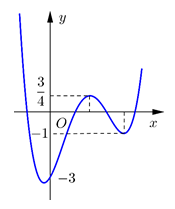
Cho hàm số bậc bốn \[y = f\left( x \right)\] có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình \[f\left( {\left| {2020x + m} \right|} \right) = 6m + 12\] có đúng 4 nghiệm thực phân biệt. Tính tổng tất cả các phần tử của S.
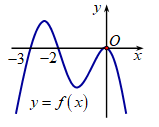
Cho hàm số f(x) liên tục trên \[\mathbb{R}.\] Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 3\] và \[x = 0\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
Trong không gian Oxyz,cho mặt phẳng \[\left( P \right):x - 4y + 3z - 2 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \[\widehat {BAC} = 60^\circ .\] Cạnh \[SC = \frac{{a\sqrt 6 }}{2}\] và vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng \[SA\] và \[BD\] bằng
Cho hình trụ (T) có chiều cao bằng 2. Một mặt phẳng (P) cắt hình trụ (T) theo thiết diện là hình chữ nhật ABCD có các cạnh \[AB,{\rm{ }}CD\] lần lượt là các dây cung của hai đường tròn đáy. Biết cạnh \[AB = AD = 2\sqrt 5 ,\] tính thể tích của khối trụ đã cho.
Chọn ngẫu nhiên một số tự nhiên A có 4 chữ số. Gọi N là số thỏa mãn \[{3^N} = A.\] Xác suất để N là số tự nhiên bằng
Cho hàm \[y = f\left( x \right) = {x^4} - 6{x^3} + 12{x^2} - \left( {2m - 1} \right)x + 3m + 2\], với m là tham số thực. Có bao nhiêu giá trị nguyên của m để hàm số \[y = f\left( {\left| x \right|} \right)\] có đúng 7 điểm cực trị?
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - 3y + 4z - 1 = 0.\] Xét mặt phẳng \[\left( Q \right):\left( {2 - m} \right)x + \left( {2m - 1} \right)y + 12z - 2 = 0,\] với m là tham số thực. Tìm tất cả các giá trị thực của m để mặt phẳng (Q) song song với mặt phẳng (P).
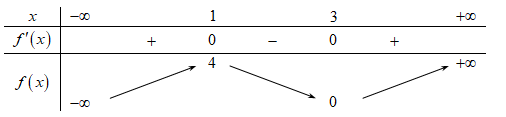
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho \[{9^x} + {9^{ - x}} = 14.\] Tính giá trị của biểu thức \[P = \frac{{6 - 3\left( {{3^x} + {3^{ - x}}} \right)}}{{12 + {3^{x + 1}} + {3^{1 - x}}}}.\]
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ. Bất phương trình \[f\left( x \right) \le {3^x} - 2x + m\] có nghiệm với mọi \[x \in \left( { - \infty ;1} \right]\] khi và chỉ khi
Trong không gian Oxyz,cho điểm \[A\left( {2; - 1; - 2} \right)\] và đường thẳng d có phương trình \[\frac{{x - 1}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 1}}{1}\]. Mặt phẳng (P) đi qua A, song song với d và khoảng cách từ d tới (P) là lớn nhất. Mặt phẳng (P) vuông góc với mặt phẳng nào dưới đây?
