Trong không gian Oxyz,cho điểm M thuộc mặt cầu (S) có phương trình \[{\left( {x - 3} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 9\] và ba điểm \[A\left( {1;0;0} \right)\], \[B\left( {2;1;3} \right)\]; \[C\left( {0;2; - 3} \right)\]. Biết rằng quỹ tích các điểm M thỏa mãn \[M{A^2} + 2\overrightarrow {MB} .\overrightarrow {MC} = 8\] là một đường tròn cố định, tính bán kính r đường tròn này.
A.\[r = \sqrt 3 .\]
B.\[r = 6.\]
C.\[r = 3.\]
D.\[r = \sqrt 6 .\]
Giải bởi Vietjack
Lời giải:
Chọn đáp án D
Mặt cầu \(\left( S \right)\)có tâm \(I\left( {3;3;2} \right)\)và bán kính \(R = 3\).
Gọi \(M\left( {x;y;z} \right)\), ta có \(M{A^2} = {\left( {1 - x} \right)^2} + {y^2} + {z^2} = {x^2} + {y^2} + {z^2} - 2{\rm{x}} + 1\).
\(\left\{ \begin{array}{l}\overrightarrow {MB} = \left( {2 - x;1 - y;3 - z} \right)\\\overrightarrow {MC} = \left( { - x;2 - y; - 3 - z} \right)\end{array} \right. \Rightarrow \overrightarrow {MB} .\overrightarrow {MC} = {x^2} + {y^2} + {z^2} - 3{\rm{x}} - 3y - 7\)
Khi đó \(M{A^2} + 2\overrightarrow {MB} .\overrightarrow {MC} = 8 \Leftrightarrow 3{{\rm{x}}^2} + 3{y^2} + 3{{\rm{z}}^2} - 6{\rm{x}} - 6y - 21 = 0\)
\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 2{\rm{x}} - 2y - 7 = 0 \Rightarrow M\) thuộc mặt cầu \(\left( {S'} \right)\) có tâm \(I'\left( {1;1;0} \right)\), bán kính \(R' = 3\).
Như vậy \(M \in \left( S \right) \cap \left( {S'} \right)\), tập hợp các điểm M thỏa mãn bài toán là đường tròn \(\left( C \right)\)có tâm Hlà trung điểm của đoạn thẳng \[II'\] (vì \(R = R' = 3\)).
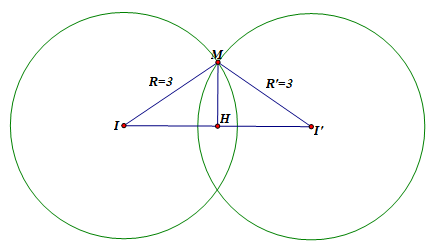
Bán kính của đường tròn \(\left( C \right)\) là \(r = \sqrt {{R^2} - I{H^2}} = \sqrt 6 \).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz,cho hai vectơ \[\vec u = \left( {1;0;2} \right)\] và \[\vec v = \left( { - 1;2;0} \right).\] Tính \[P = \cos \left( {\vec u;\vec v} \right).\]
Cho hàm số \[y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + 1\] (m là tham số thực) có hai điểm cực trị \[{x_1},{\rm{ }}{x_2}\] thỏa mãn \[x_1^2 + x_2^2 = 2.\] Mệnh đề nào dưới đây là đúng?
Cho \[a,{\rm{ }}b,{\rm{ }}x\] là các số thực dương tùy ý thỏa mãn \[{\log _2}x = 2{\log _2}a + 3{\log _2}b.\] Mệnh đề nào dưới đây là đúng?
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \left| {{x^4} - 4{x^3} - 8{x^2} - m} \right|\] có đúng 7 điểm cực trị?
Tính đạo hàm của hàm số \[y = {\log _{\frac{2}{3}}}\sqrt {{x^2} + 1} .\]
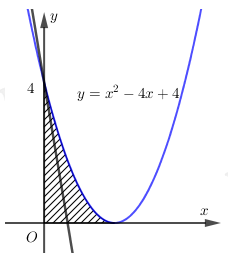
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \[y = {x^2} - 4x + 4\], trục tung và trục hoành. Xác định \[k\] để đường thẳng d đi qua điểm \[A\left( {0;4} \right)\] có hệ số góc \[k\] chia (H) thành hai phần có diện tích bằng nhau (như hình vẽ bên).
Cho hàm số f(x) có bảng biến thiên như sau:
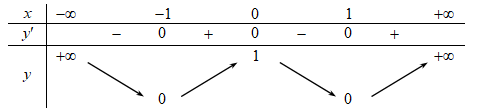
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
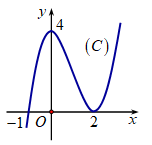
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
Biết rằng \[\int\limits_1^2 {x{{\left( {x - 1} \right)}^n}dx} = \frac{{27}}{{182}},\] với \[n \in {\mathbb{N}^*}.\] Mệnh đề nào dưới đây là đúng?
Giá trị lớn nhất của hàm số \[y = \frac{{{x^2} + 3}}{{x - 1}}\] trên đoạn \[\left[ { - 2;0} \right]\] bằng
Cho hai số phức \[{z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 - 3i.\] Số phức \[w = {z_1} - {z_2}\] có phần ảo bằng
Cho hàm số f(x) có bảng biến thiên như sau:
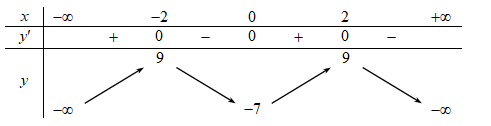
Giá trị cực đại của hàm số đã cho là
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):x - 2y + 3z - 4 = 0.\] Xét mặt phẳng \[\left( Q \right):4x + \left( {m - 1} \right)y + \left( {8 - m} \right)z - 3 = 0,\] với m là tham số thực. Tìm tất cả các giá trị thực của m để mặt phẳng (Q) vuông góc với mặt phẳng (P).
