Trong không gian Oxyz, cho hai đường thẳng \(d:\frac{{x - 1}}{1} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 1}}{1}\) và \(d':\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z + 1}}{1}\). Mặt phẳng \(\left( P \right):ax + by + cz + 2 = 0\) chứa d và tạo với \(d'\) một góc lớn nhất. Tính a + b + c.
Giải bởi Vietjack
Đáp án B
Lấy \(A\left( {1; - 2;1} \right) \in d\), qua A kẻ \(d''//d' \Rightarrow d'':\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z - 1}}{1}\).
Lấy \(I\left( {0; - 3;0} \right) \in d''\), kẻ \(IH \bot \left( P \right),{\rm{ }}IK \bot d\) (K cố định và H thay đổi).
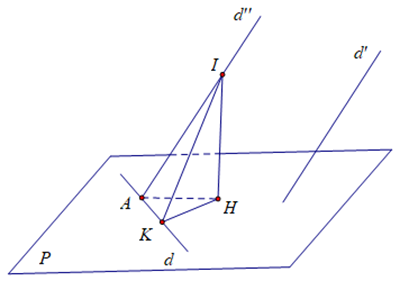
Ta có \(\left( {\widehat {d';\left( P \right)}} \right) = \left( {\widehat {d'';\left( P \right)}} \right) = \widehat {IAH}\) mà \(\sin \widehat {IAH} = \frac{{IH}}{{IA}} \le \frac{{IK}}{{IA}}\left( {const} \right)\).
Dấu “=” xảy ra \(H \equiv K{\rm{ hay }}IK \bot \left( P \right)\).
Điểm \(K \in \left( d \right) \Rightarrow K\left( {t + 1; - t - 2;t + 1} \right) \Rightarrow \overrightarrow {IK} = \left( {t + 1;1 - t;t + 1} \right)\).
Khi đó
\(IK \bot d \Rightarrow \overrightarrow {IK} .\overrightarrow {{u_d}} = 0 \Leftrightarrow \left( {t + 1} \right) - \left( {1 - t} \right) + \left( {t + 1} \right) = 0 \Leftrightarrow t = - \frac{1}{3} \Rightarrow \overrightarrow {IK} = \left( {\frac{2}{3};\frac{4}{3};\frac{2}{3}} \right)\).
Mặt phẳng \(\left( P \right)\) nhận \(\overrightarrow {IK} = \left( {\frac{2}{3};\frac{4}{3};\frac{2}{3}} \right)\) là một VTPT nên nhận \(\overrightarrow n \left( {1;2;1} \right)\) là một VTPT.
Kết hợp \(\left( P \right)\) qua \(A\left( {1; - 2;1} \right) \Rightarrow \left( P \right):\left( {x - 1} \right) + 2\left( {y + 2} \right) + \left( {z - 1} \right) = 0 \Leftrightarrow x + 2y + z + 2 = 0\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng SC và mặt phẳng \(\left( {ABC} \right)\) bằng
Cho hàm số \(f\left( x \right)\) có \(f\left( 3 \right) = - \frac{{25}}{3}\) và \(f'\left( x \right) = \frac{x}{{\sqrt {x + 1} - 1}}\). Khi đó \(\int\limits_3^8 {f\left( x \right)dx} \) bằng
Với a là số thực dương tùy ý, \(\ln \left( {8a} \right) - \ln \left( {3a} \right)\) bằng
Tìm tập xác định D của hàm số \(y = {\log _{\frac{1}{2}}}\left( {{x^2} - 6x + 8} \right)\).
Trong không gian Oxyz, cho điểm \[A\left( {1; - 1;3} \right)\] và hai đường thẳng \({d_1}:\frac{{x - 4}}{1} = \frac{{y + 2}}{4} = \frac{{z - 1}}{{ - 2}}\), \({d_2}:\frac{{x - 2}}{1} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 1}}{1}\). Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng \[{d_1}\] và cắt đường thẳng \[{d_2}\].
Trong không gian Oxyz, cho ba điểm \(A\left( {2;0;0} \right),{\rm{ }}B\left( {0;4;0} \right),{\rm{ }}C\left( {0;0;6} \right)\). Điểm M thay đổi trên mặt phẳng \(\left( {ABC} \right)\) và N là điểm trên tia \(OM.ON = 12\). Biết rằng khi M thay đổi, điểm N luôn thuộc một mặt cầu cố định. Tính bán kính của mặt cầu đó.
Cho hình chóp tứ giác đều có cạnh đáy bằng 1 và chiều cao bằng 2. Kí hiệu \(\left( H \right)\) là khối đa điện có các đỉnh là trung điểm tất cả các cạnh của hình chóp đã cho. Tính thể tích của \(\left( H \right)\).
Cho số phức z thỏa mãn \(\left| {z - 1 - i} \right| = 2\). Biết rằng giá trị nhỏ nhất của \({\left| {z + 3 + i} \right|^2} + {\left| {z - 3 + 3i} \right|^2}\) có dạng \(a + b\sqrt {10} \) với \(a,b \in \mathbb{Z}\). Tính \(a + b\).
Cho phương trình \({\log _{\frac{1}{2}}}\left( {m - 4x} \right) + 2{\log _2}\left( {x + 2} \right) = 0\). Giá trị của m để phương trình có nghiệm trên đoạn \(\left[ {2;5} \right]\) là
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
|
\(x\) |
\( - \infty \) |
|
0 |
|
2 |
|
\( + \infty \) |
|
\(f'\left( x \right)\) |
|
- |
0 |
+ |
0 |
- |
|
|
\(f\left( x \right)\) |
\( + \infty \) |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
\( - \infty \) |
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = {5^x}\) là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, cạnh \(AC = 3,{\rm{ }}BC = 4\). Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ trọng tâm của tam giác SAB đến mặt phẳng \(\left( {SBC} \right)\) bằng
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):y - 2z + 1 = 0\) và đường thẳng \(d:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 1}} = \frac{z}{1}\). Mặt phẳng \(\left( Q \right):ax + by + cz - 7 = 0\) đi qua điểm \(A\left( {2;3; - 1} \right)\), đồng thời vuông góc với mặt phẳng \(\left( P \right)\) và song song với đường thẳng d. Tính \(a + b + c\).
Trên giá sách có 10 cuốn sách Toán khác nhau, 8 cuốn sách Vật Lý khác nhau và 6 cuốn sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai cuốn sách khác nhau?
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
|
\(x\) |
\( - \infty \) |
|
0 |
|
4 |
|
\( + \infty \) |
|
\(f'\left( x \right)\) |
|
- |
0 |
+ |
0 |
- |
|
|
\(f\left( x \right)\) |
\( + \infty \) |
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-7 |
|
|
|
\( - \infty \) |
Phương trình \(2f\left( x \right) + 17\) có số nghiệm thực là
