Trong hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau: ${d_1}$: $\frac{{x - 2}}{2} = \frac{{y + 2}}{1} = \frac{{z - 6}}{{ - 2}}$, ${d_2}$: $\frac{{x - 4}}{1} = \frac{{y + 2}}{{ - 2}} = \frac{{z + 1}}{3}$. Phương trình mặt phẳng $\left( P \right)$ chứa ${d_1}$ và song song với ${d_2}$ là:

Hàm số $f\left( x \right) = {\log _3}\left( {{x^2} - 4x} \right)$ có đạo hàm trên miền xác định là $f'\left( x \right)$. Chọn kết quả đúng.

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\left[ {0;2} \right]$ thỏa mãn $f\left( 2 \right) = 1$, $\int\limits_0^2 {{{\left[ {f'\left( x \right)} \right]}^2}} dx = \frac{2}{7}$ và $\int\limits_0^2 {{x^2}.f\left( x \right)} dx = \frac{{40}}{{21}}$. Tính tích phân $I = \int\limits_0^2 {f\left( x \right)dx}$.

Số nghiệm thực của phương trình $2{\log _2}\left( {x - 3} \right) = 2 + {\log _{\sqrt 2 }}\sqrt {3 - 2x}$ là

Cho hàm số bậc ba $y = f\left( x \right)$ có đồ thị như hình vẽ bên:

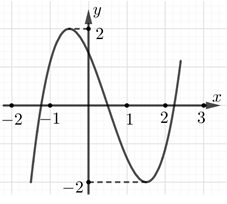
Số nghiệm thực của phương trình $f\left( {\left| {f\left( x \right)} \right|} \right) = 0$ là

Tìm giá trị nhỏ nhất của hàm số $y = \frac{{{x^2} + 3}}{{x - 1}}$ trên đoạn $\left[ {2;4} \right]$

Cho một hộp đựng 12 viên bi, trong đó có 7 viên bi đỏ, 5 viên bi xanh. Lấy ngẫu nhiên một lần 3 viên bi. Tính xác xuất lấy được ít nhất 2 viên bi màu xanh.

Nếu cấp số nhân $\left( {{u_n}} \right)$ có công bội q và ${u_1} = \frac{1}{2}$, ${u_5} = 8$ thì

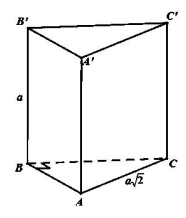
Cho khối lăng trụ đứng $ABC.A'B'C'$ có $BB' = a$, đáy ABC là tam giác vuông cân tại B, $AC = a\sqrt 2$. Tính thể tích lăng trụ

Phương trình ${9^x} - {3^{x + 1}} + 2 = 0$ có hai nghiệm ${x_1}$; ${x_2}$ với ${x_1} < {x_2}$. Đặt $P = 2{x_1} + 3{x_2}$. Khi đó:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, $AB = BC = a$, $AD = 2a$. Tam giác SAD đều và nằm trong mặt phẳng vuông góc với đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABC theo a.

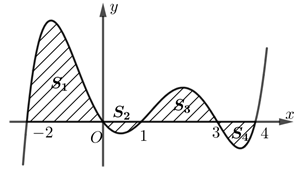
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ có đồ thị tạo với trục hoành các miền có diện tích là ${S_1}$, ${S_2}$, ${S_3}$, ${S_4}$ như hình vẽ. Biết ${S_1} = 6$, ${S_2} = 1$, ${S_3} = 4$, ${S_4} = 2$ tích phân $I = \int\limits_0^{\ln 2} {{e^x}f\left( {3{e^x} - 2} \right)dx}$ bằng

Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính thể tích của khối chóp S.ABCD theo a.

Cho hàm số $y = f\left( x \right) = {x^3} - 3{x^2} + 2$có đồ thị như hình 1

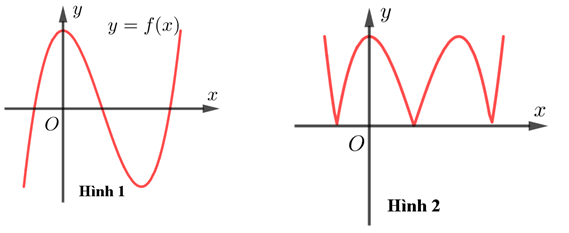
Hình 2 là đồ thị của hàm số nào trong các hàm số sau đây?

Cho hàm số $y = f\left( x \right)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số $y = - 2f\left( x \right)$ là

Trong không gian với hệ tọa độ Oxyz cho hai điểm $A\left( {1;2; - 1} \right)$, $B\left( {2;1;0} \right)$ và mặt phẳng $\left( P \right)$: $2x + y - 3z + 1 = 0$. Gọi $\left( Q \right)$ là mặt phẳng chứa A; B và vuông góc với $\left( P \right)$. Phương trình mặt phẳng $\left( Q \right)$ là: