Trong không gian tọa độ Oxyz, cho điểm \[A\left( {1;1; - 2} \right)\] thuộc mặt cầu \[\left( S \right):\;{x^2} + {\left( {y + 1} \right)^2} + {z^2} = 9.\] Từ điểm A kẻ 3 dây cung \[AB,\;AC,\;AD\] của mặt cầu (S) có độ dài bằng nhau và đôi một tạo với nhau góc \[{60^0}.\] Mặt phẳng \[\left( {BCD} \right)\] có phương trình là \[x + by + cz + d = 0.\] Khi đó \[b + c + d\] bằng
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
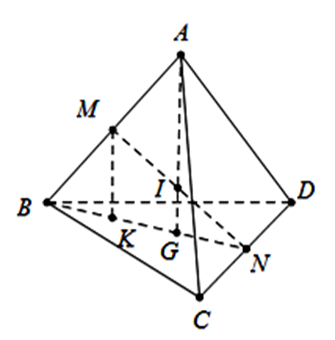
Ta có \[AB = AC = A{\rm{D}}\] và đôi một tạo với nhau góc \(60^\circ \) nên tứ giác ABCD đều. Gọi M, N lần lượt là trung điểm của AB và CD thì trọng tâm tứ diện ABCD là trung điểm của MN và cũng là tâm mặt cầu ngoại tiếp tứ diện ABCD ta có \(I\left( {0; - 1;0} \right)\).
Gọi G là trọng tâm tam giác BCD và dựng \(MK{\rm{ // AG}}\) (hình vẽ).
Ta có: \(MK = 2GI\) và \(AG = 2MK\) (tính chất đường trung bình)
Suy ra \(AG = 4IG \Rightarrow \overrightarrow {AG} = 4\overrightarrow {IG} \Rightarrow \left\{ \begin{array}{l}{x_G} - 1 = 4\left( {{x_G} - 0} \right)\\{y_G} - 1 = 4\left( {{y_G} + 1} \right)\\{z_G} + 2 = 4\left( {{z_G} - 0} \right)\end{array} \right.\)
\( \Rightarrow G\left( { - \frac{1}{3}; - \frac{5}{3};\frac{2}{3}} \right) \Rightarrow \left( {BC{\rm{D}}} \right)\) qua G và có VTPT là \(\overrightarrow n = \overrightarrow {AI} \left( { - 1; - 2;2} \right) = - \left( {1;2; - 2} \right)\)
\( \Rightarrow \left( {BC{\rm{D}}} \right):x + 2y - 2{\rm{z}} + 5 = 0\) suy ra \(b = 2,c = - 2,d = 5 \Rightarrow b + c + d = 5\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số f(x) có đạo hàm liên tục trên \[\mathbb{R}.\] Biết \[f\left( 2 \right) = 3\] và \[\int\limits_{ - 1}^3 {f\left( {\sqrt {x + 1} } \right)dx} = 4,\] khi đó \[\int\limits_0^2 {{x^2}f'\left( x \right)dx} \] bằng
Cho số phức z thỏa mãn \[\left| {\frac{{z - 1}}{{z + 3i}}} \right| = \frac{1}{{\sqrt 2 }}.\] Tìm giá trị lớn nhất của biểu thức \[P = \left| {z + i} \right| + 2\left| {\bar z - 4 + 7i} \right|.\]
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng a (tham khảo hình vẽ) . Giá trị sin của góc giữa hai mặt phẳng \[\left( {BDA'} \right)\] và \[\left( {ABCD} \right)\] bằng
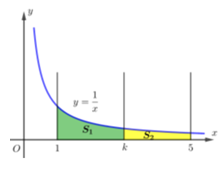
Cho hình thang cong (H) giới hạn bởi các đường \[y = \frac{1}{x},{\mkern 1mu} y = 0,{\mkern 1mu} x = 1,{\mkern 1mu} x = 5.\] Đường thẳng \[x = k\] với \[1 < k < 5\] chia (H) thành hai phần là \[\left( {{S_1}} \right)\] và \[\left( {{S_2}} \right)\] quay quanh trục \[Ox\] ta thu được hai khối tròn xoay có thể tích lần lượt là \[{V_1}\] và \[{V_2}.\] Xác định k để \[{V_1} = 2{V_2}.\]
Số nghiệm của phương trình \[{\log _2}\left( {\frac{{{{5.2}^x} - 8}}{{{2^x} + 2}}} \right) = 3 - x\] là:
Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích \[200{m^3}\] . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m2. Chi phí thuê công nhân thấp nhất là:
Số hạng không chứa x trong khai triển \[{\left( {\sqrt[3]{x} + \frac{1}{{\sqrt[4]{x}}}} \right)^7}\] bằng:
Trong không gian với hệ trục tọa độ Oxyz, cho điểm \[M\left( { - 3;3; - 3} \right)\] thuộc mặt phẳng \[\left( \alpha \right):2x - - 2y + z + 15 = 0\] và mặt cầu \[\left( S \right):{(x - 2)^2} + {(y - 3)^2} + {(z - 5)^2} = 100\]. Đường thẳng Δ qua M, nằm trên mặt phẳng (α) cắt (S) tại A, B sao cho độ dài AB lớn nhất. Viết phương trình đường thẳng Δ.
Gọi \[{z_1}\], \[{z_2}\] là hai nghiệm phức của phương trình \[3{z^2} - z + 2 = 0\]. Tính \[T = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\].
Cho hàm số \[f\left( x \right) = {\log _2}\left( {{x^2} + 1} \right)\], tính \[f'\left( 1 \right)\].
Cho khối chóp S.ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại \[C,{\mkern 1mu} \widehat {BCD} = {120^0},{\mkern 1mu} SA \bot \left( {ABCD} \right){\mkern 1mu} ,{\mkern 1mu} SA = a.\] Mặt phẳng (P) đi qua A và vuông góc với SC cắt các cạnh \[SB,SC,SD\] lần lượt tại \[M,N,P.\] Tính thể tích khối chóp \[S.AMNP\]
Tích tất cả các nghiệm của phương trình \[{3^{{x^2} + x}} = 9\] bằng
Cho hình chóp đều S.ABCD có cạnh \[AB = a\], góc giữa đường thẳng SA và mặt phẳng \[\left( {ABC} \right)\] bằng \[45^\circ \]. Thể tích khối chóp S.ABCD là
Cho hình hộp chữ nhật có độ dài các cạnh là 3, 4, 5. Nối tâm 6 mặt của hình hộp chữ nhật ta được khối 8 mặt. Thể tích của khối 8 mặt đó là
Cho đồ thị \[\left( C \right):y = {x^3} - 3{x^2}.\] Có bao nhiêu số nguyên \[b \in \left( { - 10;10} \right)\] để có đúng một tiếp tuyến của (C) đi qua điểm \[B\left( {0;b} \right)?\]