Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như hình sau:
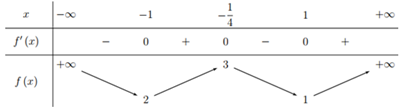
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[{2.6^{f\left( x \right)}} + \left( {{f^2}\left( x \right) - 1} \right){.9^{f\left( x \right)}} - {3.4^{f\left( x \right)}}.m \ge \left( {2{m^2} + 2m} \right){.2^{2f\left( x \right)}}\] nghiệm đúng với mọi \[x \in \mathbb{R}\]?
Giải bởi Vietjack
Đáp án D
\({2.6^{f\left( x \right)}} + \left( {{f^2}\left( x \right) - 1} \right){.9^{f\left( x \right)}} - {3.4^{f\left( x \right)}}.m \ge \left( {2{m^2} + 2m} \right){.2^{2f\left( x \right)}},\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left( {{f^2}\left( x \right) - 1} \right){.9^{f\left( x \right)}} + {2.6^{f\left( x \right)}} - \left( {2{m^2} + 5m} \right){.4^{f\left( x \right)}} \ge 0,\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left( {{f^2}\left( x \right) - 1} \right).{\left( {\frac{9}{4}} \right)^{f\left( x \right)}} + 2.{\left( {\frac{3}{2}} \right)^{f\left( x \right)}} - 2{m^2} - 5m \ge 0,\forall x \in \mathbb{R}\)
\( \Leftrightarrow 2{m^2} + 5m \le \left( {{f^2}\left( x \right) - 1} \right).{\left( {\frac{9}{4}} \right)^{f\left( x \right)}} + 2.{\left( {\frac{3}{2}} \right)^{f\left( x \right)}},\forall x \in \mathbb{R}\) (1)
Đặt \(t = f\left( x \right) \ge 1,{\rm{ }}\forall {\rm{x}} \in \mathbb{R}\). (1) thành: \(2{m^2} + 5m \le \left( {{t^2} - 1} \right){\left( {\frac{9}{4}} \right)^t} + 2{\left( {\frac{3}{2}} \right)^t},\forall t \in \left[ {1; + \infty } \right)\)
Đặt \(g\left( t \right) = \left( {{t^2} - 1} \right).{\left( {\frac{9}{4}} \right)^t} + 2{\left( {\frac{3}{2}} \right)^t},\forall t \in \left[ {1; + \infty } \right)\)
\( \Rightarrow g'\left( t \right) = 2t.{\left( {\frac{9}{4}} \right)^t} + \left( {{t^2} - 1} \right).{\left( {\frac{9}{4}} \right)^t}\ln \frac{9}{4} + 2.{\left( {\frac{3}{2}} \right)^t}\ln \frac{3}{2} > 0,\forall t \in \left[ {1; + \infty } \right)\)
Suy ra \(g\left( t \right) \ge g\left( 1 \right) = 3,\forall t \in \left[ {1; + \infty } \right)\).
Yêu cầu bài toán \( \Leftrightarrow 2{m^2} + 5m \le 3 \Leftrightarrow - 3 \le m \le \frac{1}{2}\).
Do \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 3; - 2; - 1;0} \right\}\) nên có 4 giá trị nguyên thỏa mãn.
Gói VIP thi online tại VietJack (chỉ 200k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số f(x) có bảng biến thiên như sau:
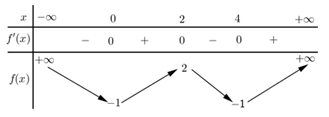
Số nghiệm thuộc khoảng \[\left( {0;\pi } \right)\] của phương trình \[3f\left( {2 + 2\cos x} \right) - 4 = 0\] là
Cho hình chóp S.ABCD có SA vuông góc với đáy, \[SA = a\sqrt 6 .\] Đáy ABCD là hình thang vuông tại A và \[B,{\mkern 1mu} {\mkern 1mu} AB = BC = \frac{1}{2}AD = a.\] Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp \[S.ECD\].
Cho khối chóp S.ABCD có đáy là hình chữ nhật, \[AB = a\], \[AD = a\sqrt 3 \], SA vuông góc với đáy và mặt phẳng \[\left( {SBC} \right)\] tạo với đáy một góc \[60^\circ \]. Tính thể tích V của khối chóp S.ABCD.
Cho số phức \[z = 1 + 2i\] . Tìm tổng phần thực và phần ảo của số phức \[w = 2z + \bar z\] .
Tính nguyên hàm \[I = \int {\frac{{x - 5}}{{{x^2} - 1}}{\rm{d}}x} \]
Gọi S là tập nghiệm của phương trình \[2{\log _2}\left( {2x - 2} \right) + {\log _2}{\left( {x - 3} \right)^2} = 2\] trên \[\mathbb{R}.\] Tổng các phần tử của S bằng
Cho cấp số cộng có số hạng thứ 3 và số hạng thứ 7 lần lượt là 6 và – 2. Tìm số hạng thứ 5.
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
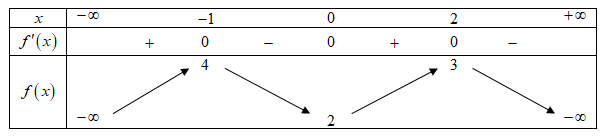
Bất phương trình \[\left( {{x^2} + 1} \right)f\left( x \right) \ge m\] có nghiệm trên khoảng \[\left( { - 1;2} \right)\] khi và chỉ khi
Từ một nhóm có 10 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra 2 học sinh nam và 3 học sinh nữ để lập thành một đội 5 bạn đi biễu diễn văn nghệ
Cho số phức \[z = a + bi\] với \[a,b \in \mathbb{R}\] thỏa mãn \[\left( {1 + 3i} \right)z + \left( {2 + i} \right)\bar z = - 2 + 4i.\] Tính \[P = ab.\]
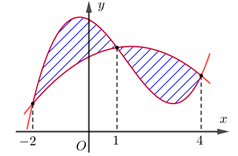
Cho hai hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + 5\] và \[g\left( x \right) = d{x^2} + ex + 3\;\left( {a,b,c,d,e \in \mathbb{R}} \right).\] Biết rằng đồ thị của hàm số \[y = f\left( x \right)\] và \[y = g\left( x \right)\] cắt nhau tại 3 điểm có hoành độ lần lượt là \[ - 2,\;1,\;4\] (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
Cho đường thẳng Δ đi qua điểm \[M\left( {2;0; - 1} \right)\] và vecto chỉ phương \[\vec a = \left( {4; - 6;2} \right)\]. Phương trình tham số của đường thẳng Δ là
Cho \[{\log _a}b = 2\] và \[{\log _a}c = 3\]. Tính \[P = {\log _a}\left( {\frac{{{b^3}}}{{{c^2}}}} \right)\].
Cho hàm số \[f\left( x \right),\] có bảng xét dấu \[f'\left( x \right)\] như sau
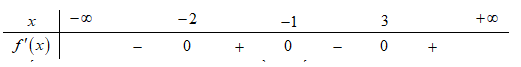
Hàm số \[y = f\left( {{x^2} - 2x} \right)\] đồng biến trên khoảng nào dưới dây
Cho hình chóp S.ABCD có các mặt phẳng \[\left( {SAB} \right),\left( {SAD} \right)\] cùng vuông góc với mặt phẳng \[\left( {ABCD} \right)\], đáy là hình thang vuông tại các đỉnh A và B, có \[AD = 2AB = 2BC = 2a\], \[SA = AC\]. Khoảng cách giữa hai đường thẳng SB và CD bằng:
