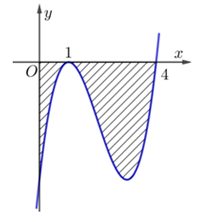
Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với góc \[{60^0}.\] Gọi M là trung điểm của SC. Mặt phẳng qua AM và song song với BD, cắt \[SB,SD\] lần lượt tại E và F và chia khối chóp thành hai phần. Tính thể tích V của khối chóp không chứa đỉnh S.
Giải bởi Vietjack
Đáp án B
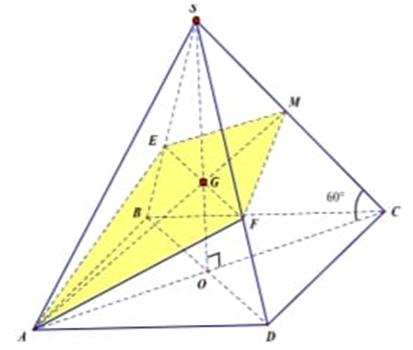
+) Gọi \(O = AC \cap BD,{\rm{ }}G = AM \cap SO\)
Þ G là trọng tâm \(\Delta SAC \Rightarrow \frac{{SG}}{{SO}} = \frac{2}{3}\).
+) Ta có: \(\left( {\widehat {SC;\left( {ABCD} \right)}} \right) = \left( {\widehat {SC;OC}} \right) = \widehat {SCO} = 60^\circ \)
Có \(OC = \frac{1}{2}.AC = \frac{{a\sqrt 2 }}{2},{\rm{ }}SO = OC.\tan \widehat {SCO} = \frac{{a\sqrt 2 }}{2}\tan 60^\circ = \frac{{a\sqrt 6 }}{2}\)
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{{a\sqrt 6 }}{2}.{a^2} = \frac{{{a^3}\sqrt 6 }}{3}\).
+) Gọi \(\left( \alpha \right)\) là mặt phẳng chứa AM và song song với BD Þ \(\left( \alpha \right)\) là mặt phẳng đi qua G và song song với BD và cắt SB, SD lần lượt tại E và F. Do đó \(\left( \alpha \right)\) cắt hình chóp S.ABCD theo thiết diện là tứ giác AEMF Þ \(\left( \alpha \right)\) chia khối chóp S.ABCD thành hai phần là khối chóp S.AEMF và khối đa diện EMFABCD.
+) Ta có EF đi qua G và \(EF//BD \Rightarrow \frac{{SE}}{{SB}} = \frac{{SF}}{{SD}} = \frac{{SG}}{{SO}} = \frac{2}{3}\).
+) \(\frac{{{V_{S.AEF}}}}{{{V_{S.ABD}}}} = \frac{{SE}}{{SB}}.\frac{{SF}}{{SD}} = \frac{2}{3}.\frac{2}{3} = \frac{4}{9} \Rightarrow {V_{S.ABD}} = \frac{2}{9}{V_{S.ABCD}}\)
+) \(\frac{{{V_{S.EFM}}}}{{{V_{S.BCD}}}} = \frac{{SE}}{{SB}}.\frac{{SF}}{{SD}}.\frac{{SM}}{{SC}} = \frac{2}{3}.\frac{2}{3}.\frac{1}{2} = \frac{2}{9} \Rightarrow {V_{S.EFM}} = \frac{2}{9}{V_{S.BCD}} = \frac{1}{9}{V_{S.ABCD}}\)
+ Ta có: \({V_{S.AEMF}} = {V_{S.AEF}} + {V_{S.EFM}} = \frac{1}{3}{V_{S.ABCD}}\)
Þ Thể tích khối chóp không chứa đỉnh S là:
\(V = {V_{S.ABCD}} - {V_{S.AEMF}} = \frac{2}{3}{V_{S.ABCD}} = \frac{2}{3}.\frac{{{a^3}\sqrt 6 }}{6} = \frac{{{a^3}\sqrt 6 }}{9}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):2x + 2y - z + 9 = 0\] và điểm \[A\left( {1;2; - 3} \right).\] Đường thẳng d đi qua A và có vectơ chỉ phương \[\vec u = \left( {3;4; - 4} \right)\] cắt (P) tại B. Điểm M thay đổi trên (P) sao cho M luôn nhìn đoạn AB dưới một góc \[{90^0}\]. Độ dài đoạn MB lớn nhất bằng
Cho hàm số \[y = f\left( x \right)\] là hàm số bậc ba có bảng biến thiên như hình vẽ
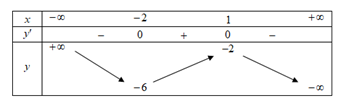
Số đường tiệm cận đứng và ngang của đồ thị hàm số \[y = \frac{{2x + 7 - 3\sqrt {4x + 5} }}{{\left| {f\left( x \right)} \right| - 2}}\] là
Một chất điểm đang chuyển động với vận tốc \[{v_0} = 15{\mkern 1mu} m/s\] thì tăng tốc với gia tốc \[a\left( t \right) = {t^2} + 4t{\mkern 1mu} \left( {m/{s^2}} \right).\] Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc.
Cho hàm số \[y = f\left( x \right)\] có bảng xét dấu của đạo hàm như sau.
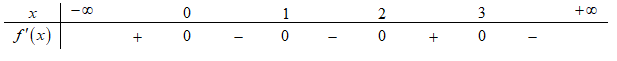
Hàm số \[y = f\left( {x - 1} \right) + {x^3} - 12x + 2019\] nghịch biến trên khoảng nào dưới đây?
Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC, với \[A\left( {1;2;1} \right),B\left( { - 3;0;3} \right),C\left( {2;4; - 1} \right).\] Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
Cho tích phân \[I = \int\limits_0^4 {f\left( x \right)dx} = 32.\] Tính tích phân \[J = \int\limits_0^2 {f\left( {2x} \right)dx} \].
Cho số phức z thỏa mãn \[(2 + 3i)z + 4 - 3i = 13 + 4i\]. Môđun của z bằng
Trong không gian Oxyz, cho mặt cầu \[(S):{(x + 2)^2} + {(y - 1)^2} + {(z + \sqrt 2 )^2} = 9\] và hai điểm \[A( - 2;0; - 2\sqrt 2 ),B( - 4; - 4;0)\]. Biết rằng tập hợp các điểm M thuộc \[(S)\] sao cho \[M{A^2} + \overrightarrow {MO} .\overrightarrow {MB} = 16\] là một đường tròn. Bán kính của đường tròn đó bằng
Trong không gian Oxyz, cho \[A\left( {1;3;5} \right)\], \[B\left( { - 5; - 3; - 1} \right)\]. Phương trình mặt cầu đường kính AB là:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật \[AB = a\], \[AD = 2a\], cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng \[\frac{{2{a^3}}}{3}\] . Tính góc tạo bởi đường thẳng SB với mặt phẳng \[\left( {ABCD} \right)\].
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh a. Gọi M, N lần lượt là trung điểm của cạnh \[A'B'\] và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnhA và \[(H')\] là khối đa diện còn lại. Tính tỉ số \[\frac{{{V_{(H)}}}}{{{V_{(H')}}}}.\]
Tìm họ nguyên hàm của hàm số \[y = {x^2} - {3^x} + \frac{1}{x}.\]
Với các số thực \[a,b > 0,a \ne 1\] tùy ý, biểu thức \[{\log _{{a^2}}}\left( {a{b^2}} \right)\] bằng:
