Trong không gian Oxyz, cho mặt phẳng (P):x+y−z−3=0 và hai điểm A(1;1;1), B(−3;−3;−3). Mặt cầu (S) đi qua hai điểm A,B và tiếp xúc với (P) tại điểm C. Biết rằng C luôn thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Gọi I=AB∩(P).
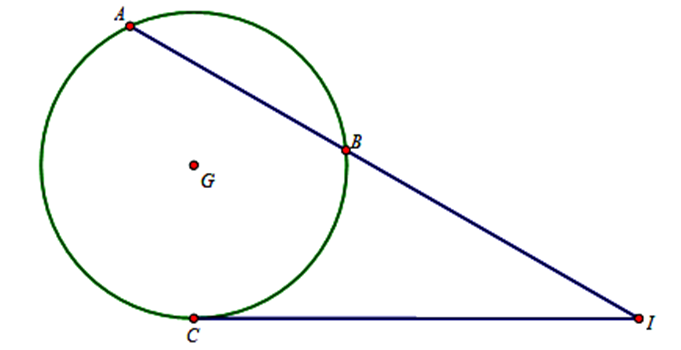
Ta có →BA=(4;4;4)=4(1;1;1)⇒AB:{x=1+ty=1+tz=1+t⇒I(t+1;t+1;t+1).
Mà I∈(P)⇒(t+1)+(t+1)−(t+1)−3=0⇔t=2⇒I(3;3;3)
⇒{→IA=(−2;−2;−2)→IB=(−6;−6;−6)⇒{IA=2√3IB=6√3
Mặt cầu (S) tiếp xúc với (P) tại C nên IC là tiếp tuyến của (S).
Do đó IA.IB=IC2⇒IC=√IA.IB=6⇒C thuộc mặt cầu có tâm I(3;3;3) và bán kính R=IC=6.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y=mx+7m−8x−m, với m là tham số thực. Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên từng khoảng xác định?
Biết rằng 4∫2x3+2x2+xdx=a+bln2+cln3+dln5, với a,b,c,d∈Z. Tính giá trị của biểu thức S=a+b+c+d.
Có bao nhiêu số phức z thỏa mãn \left( {1 + i} \right)z + \bar z là số thuần ảo và \left| {z - 2i} \right| = 1?
Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.
Trong không gian Oxyz, cho đường thẳng d:\left\{ \begin{array}{l}x = 2 + t\\y = - 1\\z = 3 + 2t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right). Đường thẳng d đi qua điểm có tọa độ nào dưới đây?
Họ tất cả các nguyên hàm của hàm số f\left( x \right) = {e^{4x + 3}} là
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Khoảng cách từ điểm A đến mặt phẳng \left( {SBC} \right) bằng
Cho \int\limits_0^1 {f\left( x \right)dx} = 2 và \int\limits_1^2 {f\left( x \right)dx} = - 3. Tích phân \int\limits_0^2 {f\left( x \right)dx} bằng
Tìm tập xác định D của hàm số y = {\left( {{x^2} - 6x + 8} \right)^{\frac{1}{{2020}}}}.
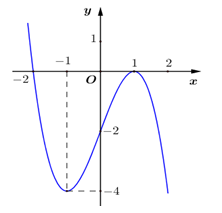
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Cho ba số phức {z_1},{\rm{ }}{z_2},{\rm{ }}{z_3} thỏa mãn \left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1; \left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2} và z_1^2 = {z_2}{z_3}. Tính giá trị của \left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right|.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:\left\{ \begin{array}{l}x = 3 + 3t\\y = 4 + 2t\\z = 2 + t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right). Xét đường thẳng \Delta :\frac{{x - 2}}{6} = \frac{{y - 1}}{4} = \frac{{z + 3}}{m}, với m là tham số thực khác 0. Tìm tất cả các giá trị thực của m để đường thẳng \Delta song song với đường thẳng d.
Trong không gian, cho hình thang cân ABCD có đáy nhỏ AB = 1, đáy lớn CD = 3 và cạnh bên AD = \sqrt 2 . Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD xung quanh trục AB.
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức z = - 1 - 2i?