Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 29)
-
6232 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho a là số thực dương tùy ý và \[a \ne 1.\] Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có \({\log _3}a = \frac{1}{{{{\log }_a}3}}\).
Câu 2:
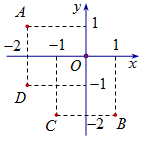
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \[z = - 1 - 2i\]?
 Xem đáp án
Xem đáp án
Đáp án C
Điểm biểu diễn số phức \(z = - 1 - 2i\) có tọa độ \(\left( { - 1;2} \right)\).
Câu 3:
Cho \[\int\limits_0^1 {f\left( x \right)dx} = 2\] và \[\int\limits_1^2 {f\left( x \right)dx} = - 3.\] Tích phân \[\int\limits_0^2 {f\left( x \right)dx} \] bằng
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \(\int\limits_0^2 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^2 {f\left( x \right)d{\rm{x}}} = - 1\).
Câu 4:
Trong không gian Oxyz, cho hai điểm \[A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\] Tìm tọa độ của vectơ \[\overrightarrow {AB} .\]
 Xem đáp án
Xem đáp án
Đáp án B
Ta có \(\overrightarrow {AB} = \left( {4; - 1; - 2} \right)\).
Câu 5:
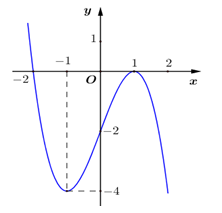
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \(y\left( 1 \right) = 0 \Rightarrow \) Loại A và B. Mà \(y\left( { - 1} \right) = - 4\).
Câu 6:
Cho số phức \[z = 1 + 2i.\] Tìm số phức \[w = {z^2} + i.\]
 Xem đáp án
Xem đáp án
Đáp án B
Ta có \[{\rm{w}} = {\left( {1 + 2i} \right)^2} + i = - 3 + 5i\].
Câu 7:
Cho hàm số f(x) có bảng biến thiên như sau:
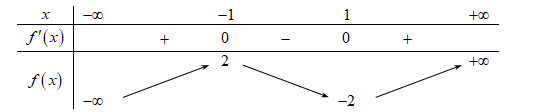
Giá trị cực đại của hàm số đã cho là
 Xem đáp án
Xem đáp án
Đáp án A
Giá trị cực đại của hàm số \(f\left( x \right)\) là 2.
Câu 8:
Cho hàm số f(x) có bảng biến thiên như sau:
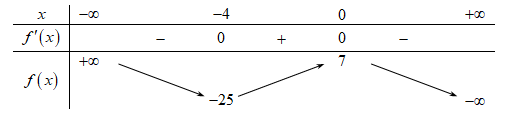
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án A
Hàm số \(f\left( x \right)\) đồng biến trên \(\left( { - 4;0} \right)\).
Câu 9:
Tìm tập xác định D của hàm số \[y = {\left( {{x^2} - 6x + 8} \right)^{\frac{1}{{2020}}}}.\]
 Xem đáp án
Xem đáp án
Đáp án C
Hàm số \(y = {\left( {{x^2} - 6{\rm{x}} + 8} \right)^{\frac{1}{{2020}}}}\) xác định \({x^2} - 6{\rm{x}} + 8 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 4\\x < 2\end{array} \right.\).
Câu 10:
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = {e^{4x + 3}}\] là
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \(\int {{e^{4{\rm{x}} + 3}}d{\rm{x}}} = \frac{1}{4}{e^{4{\rm{x}} + 3}} + C\).
Câu 11:
Trong không gian Oxyz, cho đường thẳng \[d:\left\{ \begin{array}{l}x = 2 + t\\y = - 1\\z = 3 + 2t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right).\] Đường thẳng d đi qua điểm có tọa độ nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án A
Đường thẳng d đi qua điểm có tọa độ \(\left( {2; - 1;3} \right)\).
Câu 12:
Trong một lớp học có 32 học sinh. Hỏi có bao nhiêu cách chọn 2 học sinh lên bảng kiểm tra bài cũ?
 Xem đáp án
Xem đáp án
Đáp án C
Chọn 2 học sinh lên bảng kiểm tra bài cũ từ 32 học sinh có \(C_{32}^2\) cách.
Câu 13:
Cho cấp số nhân \[\left( {{u_n}} \right)\] với \[{u_1} = 3,{\rm{ }}q = \frac{1}{2}.\] Số \[\frac{3}{{512}}\] là số hạng thứ mấy?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có \({u_n} = {u_1}{q^{n - 1}} \Rightarrow \frac{3}{{512}} = 3.{\left( {\frac{1}{2}} \right)^{n - 1}} \Leftrightarrow \frac{1}{{{2^{n - 1}}}} = \frac{1}{{512}}\)
\( \Leftrightarrow {2^{n - 1}} = 512 \Leftrightarrow n - 1 = 9 \Leftrightarrow n = 10\).
Câu 14:
Cho hình nón (N) có đường cao bằng 4 và đường sinh bằng 5. Tính thể tích V của khối nón (N).
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \(\left\{ \begin{array}{l}V = \frac{1}{3}\pi {r^2}h\\h = 4;{\rm{ }}\ell = 5;{\rm{ }}{\ell ^2} = {h^2} + {R^2}\end{array} \right. \Rightarrow r = 3 \Rightarrow V = 12\pi \).
Câu 15:
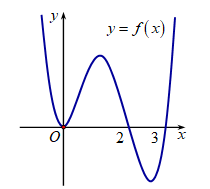
Cho hàm số f(x) liên tục trên \[\mathbb{R}.\] Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = 0\] và \[x = 3\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có \(S = \int\limits_0^2 {\left| {f\left( x \right)d{\rm{x}}} \right|} + \int\limits_2^3 {\left| {f\left( x \right)} \right|d{\rm{x}}} = \int\limits_0^2 {f\left( x \right)d{\rm{x}}} - \int\limits_2^3 {f\left( x \right)d{\rm{x}}} \).
Câu 16:
Giải phương trình \[{\left( {27\sqrt 3 } \right)^{{x^2} - x + 1}} = {9^{x + 1}}.\]
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \({\left( {27\sqrt 3 } \right)^{{x^2} - x + 1}} = {9^{x + 1}} \Leftrightarrow {\left( {{3^3}{{.3}^{\frac{1}{2}}}} \right)^{{x^2} - x + 1}} = {\left( {{3^2}} \right)^{x + 1}} \Leftrightarrow {\left( {{3^{3 + \frac{1}{2}}}} \right)^{{x^2} - x + 1}} = {3^{2\left( {x + 1} \right)}}\).
\( \Leftrightarrow {3^{\frac{7}{2}\left( {{x^2} - x + 1} \right)}} = {3^{2\left( {x + 1} \right)}} \Leftrightarrow \frac{7}{2}\left( {{x^2} - x + 1} \right) = 2\left( {x + 1} \right) \Leftrightarrow x = \frac{{11 \pm \sqrt {37} }}{{14}}.\)
Câu 17:
Kí hiệu \[{z_1},{\rm{ }}{z_2},{\rm{ }}{z_3},{\rm{ }}{z_4}\] là bốn nghiệm phức của phương trình \[{z^4} - 5{z^2} - 36 = 0.\] Giá trị của \[\left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| + \left| {{z_4}} \right|\] bằng
 Xem đáp án
Xem đáp án
Đáp án A
Ta có \({z^4} - 5{z^2} - 36 = 0 \Leftrightarrow \left( {{z^2} + 4} \right)\left( {{z^2} - 9} \right) = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{{z^2} = - 4 = 4{i^2}}\\{{z^2} = 9}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{z = \pm 2i}\\{z = \pm 3}\end{array}} \right.\)
\( \Rightarrow \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| + \left| {{z_4}} \right| = \left| {2i} \right| + \left| { - 2i} \right| + 3 + 3 = 2 + 2 + 6 = 10.\)
Câu 18:
Cho hàm số f(x) có bảng biến thiên như sau:
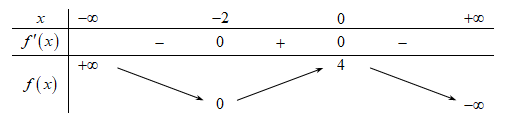
Phương trình \[2f\left( x \right) - 9 = 0\] có số nghiệm thực là
 Xem đáp án
Xem đáp án
Đáp án A
Đường thẳng \(y = \frac{9}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại đúng 1 điểm.
Câu 19:
Tìm giá trị nhỏ nhất \[{y_{\min }}\] của hàm số \[y = {x^4} - 4{x^3} + 8x.\]
 Xem đáp án
Xem đáp án
Đáp án C
Hàm số đã cho xác định trên \(\mathbb{R}\).
Ta có \(y' = 4{{\rm{x}}^3} - 12{{\rm{x}}^2} + 8;{\rm{ y'}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1 \pm \sqrt 3 \end{array} \right.\)
Xét bảng sau:
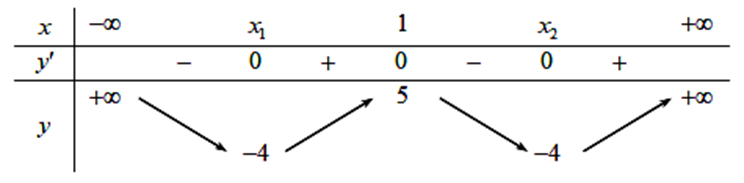
Trong đó \({x_1} = 1 - \sqrt 3 ;{\rm{ }}{{\rm{x}}_2} = 1 + \sqrt 3 \).
Từ bảng trên, ta được giá trị nhỏ nhất của hàm số đã cho bằng \( - 4\).
Câu 20:
Tổng giá trị các nghiệm thực của phương trình \[{\log _2}x.{\log _4}x.{\log _8}x.{\log _{16}}x = \frac{{32}}{3}\] bằng
 Xem đáp án
Xem đáp án
Đáp án A
Điều kiện \(x > 0\) (*). Phương trình \( \Leftrightarrow {\log _2}x.\frac{1}{2}{\log _2}x.\frac{1}{3}{\log _2}x.\frac{1}{4}{\log _2}x = \frac{{32}}{3}\)
\( \Leftrightarrow {\left( {{{\log }_2}x} \right)^4} = 256 \Leftrightarrow \left[ \begin{array}{l}{\log _2}x = 4\\{\log _2}x = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {2^4}\\x = {2^{ - 4}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\\x = \frac{1}{{16}}\end{array} \right.\).
Câu 21:
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
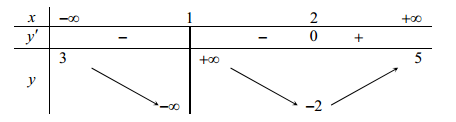
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
 Xem đáp án
Xem đáp án
Đáp án C
ĐTHS có tiệm cận đứng \(x = 1\). Từ \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } y = 3 \Rightarrow TCN:y = 3\\\mathop {\lim }\limits_{x \to + \infty } y = 5 \Rightarrow TCN:y = 5\end{array} \right.\).
Câu 22:
Tìm tất cả các giá trị của tham số m để hàm số \[y = {x^3} - m{x^2} + \left( {{m^2} - 16} \right)x + 3\] đạt cực tiểu tại điểm \[x = 0.\]
 Xem đáp án
Xem đáp án
Đáp án B
Ta có \(y' = 3{{\rm{x}}^2} - 2m{\rm{x}} + {m^2} - 16 \Rightarrow y'' = 6{\rm{x}} - 2m\).
YCBT \( \Leftrightarrow \left\{ \begin{array}{l}y'\left( 0 \right) = 0\\y''\left( 0 \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 16 = 0\\ - 2m > 0\end{array} \right. \Leftrightarrow m = - 4\).
Câu 23:
Cho hai số thực dương \[a,{\rm{ }}b\] thỏa mãn \[{\log _4}a = {\log _6}b = {\log _9}\left( {a + b} \right)\]. Tính \[\frac{a}{b}\].
 Xem đáp án
Xem đáp án
Đáp án B
Đặt \({\log _4}a = {\log _6}b = {\log _9}\left( {a + b} \right) = t \Rightarrow \left\{ \begin{array}{l}a = {4^t}\\b = {6^t}\\a + b = {9^t}\end{array} \right.\)
\( \Rightarrow {4^t} + {6^t} = {9^t} \Rightarrow {\left( {\frac{4}{9}} \right)^t} + {\left( {\frac{6}{9}} \right)^t} = 1 \Rightarrow {\left[ {{{\left( {\frac{2}{3}} \right)}^t}} \right]^2} + {\left( {\frac{2}{3}} \right)^t} - 1 = 0 \Rightarrow {\left( {\frac{2}{3}} \right)^t} = \frac{{\sqrt 5 - 1}}{2}.\)
Ta có \(\frac{a}{b} = {\left( {\frac{4}{6}} \right)^t} = {\left( {\frac{2}{3}} \right)^t} = \frac{{\sqrt 5 - 1}}{2}.\)
Câu 24:
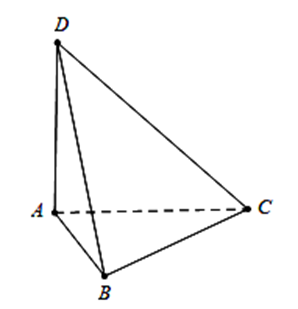
Cho tứ diện ABCD có \[AB,{\rm{ }}AC,{\rm{ }}AD\] đôi một vuông góc với nhau và diện tích các tam giác \[ABC,{\rm{ }}ABD,{\rm{ }}ACD\] lần lượt là \[3{a^2},{\rm{ }}4{a^2},{\rm{ }}6{a^2}.\] Thể tích của khối tứ diện ABCD bằng
 Xem đáp án
Xem đáp án
Đáp án C
Ta có \({V_{ABC{\rm{D}}}} = \frac{1}{6}AB.AC.A{\rm{D}}\)
\(\left\{ \begin{array}{l}{S_{ABC}} = \frac{1}{2}AB.AC = 3{a^2}\\{S_{ABD}} = \frac{1}{2}AB.AD = 4{a^2}\\{S_{ACD}} = \frac{1}{2}AC.AD = 6{a^2}\end{array} \right. \Rightarrow {\left( {AB.AC.AD} \right)^2} = 6{a^2}.8{a^2}.12{a^2}\)
\( \Rightarrow AB.AC.AD = 24{a^3} \Rightarrow {V_{ABCD}} = 4{a^3}.\)
Câu 25:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\left\{ \begin{array}{l}x = 3 + 3t\\y = 4 + 2t\\z = 2 + t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right).\] Xét đường thẳng \[\Delta :\frac{{x - 2}}{6} = \frac{{y - 1}}{4} = \frac{{z + 3}}{m},\] với m là tham số thực khác 0. Tìm tất cả các giá trị thực của m để đường thẳng \[\Delta \] song song với đường thẳng \[d.\]
 Xem đáp án
Xem đáp án
Đáp án B
Đường thẳng d qua \(A\left( {3;4;2} \right)\) và có một VTCP là \(\overrightarrow {{u_1}} = \left( {3;2;1} \right)\).
Đường thẳng \(\Delta \) có một VTCP là \(\overrightarrow {{u_2}} = \left( {6;4;m} \right)\).
YCBT \( \Leftrightarrow \left\{ \begin{array}{l}A \notin \Delta \\\frac{6}{3} = \frac{4}{2} = \frac{m}{1}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}A \notin \Delta \\m = 2\end{array} \right.\) (1)
Ta thấy ngay \(A\left( {3;4;2} \right)\) không thuộc \(\Delta :\frac{{x - 2}}{6} = \frac{{y - 1}}{4} = \frac{{z + 3}}{m}\) vì \(\frac{{3 - 2}}{6} \ne \frac{{4 - 1}}{4}\).
Khi đó (1) \( \Leftrightarrow m = 2\), thỏa mãn \(m \ne 0\).
Câu 26:
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x + y + z - 3 = 0\] và điểm \[A\left( {1;2;3} \right)\]. Điểm \[H\left( {a;b;c} \right)\] là hình chiếu vuông góc của A trên (P). Tính \[a + 2b + c.\]
 Xem đáp án
Xem đáp án
Đáp án B
Ta có AH qua \(A\left( {1;2;3} \right)\) và nhận \(\overrightarrow {{n_P}} = \left( {1;1;1} \right)\) là một VTCP
\( \Rightarrow AH:\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\\z = 3 + t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right) \Rightarrow H\left( {t + 1;t + 2;t + 3} \right)\).
Mà \(H \in \left( P \right) \Rightarrow \left( {t + 1} \right) + \left( {t + 2} \right) + \left( {t + 3} \right) - 3 = 0 \Leftrightarrow t = - 1 \Rightarrow H\left( {0;1;2} \right)\).
Câu 27:
Trong không gian, cho hình thang cân ABCD có đáy nhỏ \[AB = 1\], đáy lớn \[CD = 3\] và cạnh bên \[AD = \sqrt 2 .\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD xung quanh trục \[AB.\]
 Xem đáp án
Xem đáp án
Đáp án A
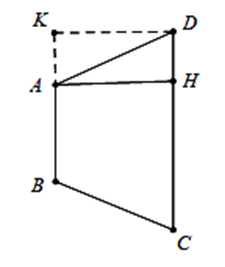
Ta có \(V = {V_{tru}} - 2{V_{non}} = \pi {r^2}h - 2.\frac{1}{3}\pi {R^2}h' = \pi .K{D^2}.CD - \frac{2}{3}\pi K{D^2}.AK.\)
Cạnh \(AK = DH = \frac{{CD - AB}}{2} = 1\)
\( \Rightarrow K{D^2} = A{D^2} - A{K^2} = 1 \Rightarrow V = \frac{7}{3}\pi .\)
Câu 28:
Cho hàm số \[y = \frac{{mx + 7m - 8}}{{x - m}}\], với m là tham số thực. Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên từng khoảng xác định?
 Xem đáp án
Xem đáp án
Đáp án A
Ta có \(y' = \frac{{ - {m^2} - 7m + 8}}{{{{\left( {x - m} \right)}^2}}} > 0,\forall x \ne m \Leftrightarrow {m^2} + 7m - 8 < 0 \Leftrightarrow - 8 < m < 1.\)
Bài ra \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}.\)
Câu 29:
Biết rằng \[\int\limits_2^4 {\frac{{{x^3} + 2}}{{{x^2} + x}}dx} = a + b\ln 2 + c\ln 3 + d\ln 5,\] với \[a,{\rm{ }}b,{\rm{ }}c,{\rm{ }}d \in \mathbb{Z}.\] Tính giá trị của biểu thức \[S = a + b + c + d.\]
 Xem đáp án
Xem đáp án
Đáp án A
Phân tích \(\frac{{{x^3} + 2}}{{{x^2} + x}} = \frac{{x\left( {{x^2} + x} \right) - \left( {{x^2} + x} \right) + x + 2}}{{{x^2} + x}} = x - 1 + \frac{{x + 2}}{{x\left( {x + 1} \right)}} = x - 1 + \frac{m}{x} + \frac{n}{{x + 1}}\)
\( \Rightarrow x + 2 = m\left( {x + 1} \right) + nx,\) cho \(\left\{ \begin{array}{l}x = 0 \Rightarrow m = 2\\x = - 1 \Rightarrow n = - 1\end{array} \right. \Rightarrow \int\limits_2^4 {\frac{{{x^3} + 2}}{{{x^2} + x}}dx} = \int\limits_2^4 {\left( {x - 1 + \frac{2}{x} - \frac{1}{{x + 1}}} \right)dx} \)
\( \Rightarrow I = \left. {\left( {\frac{{{x^2}}}{2} - x + 2\ln \left| x \right| - \ln \left| {x + 1} \right|} \right)} \right|_2^4 = \left( {4 + 2\ln 4 - \ln 5} \right) - \left( {2\ln 2 - \ln 3} \right)\)
\( = 4 + 2\ln 2 + \ln 3 - \ln 5 \Rightarrow a = 4,{\rm{ }}b = 2,{\rm{ }}c = 1,{\rm{ }}d = - 1 \Rightarrow S = 6.\)
Câu 30:
Cho phương trình \[\log _2^2x - m{\log _2}x + m + 2 = 0\] (m là tham số thực) có hai nghiệm thực phân biệt \[{x_1},{\rm{ }}{x_2}\] thỏa mãn \[{x_1}{x_2} = 64.\] Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Điều kiện: \(x > 0\) (*). Đặt \(t = {\log _2}x \Rightarrow {t^2} - mt + m + 2 = 0\) và \(x = {2^t}\).
Ép cho \(\left\{ \begin{array}{l}\Delta = {m^2} - 4\left( {m + 2} \right) > 0\\{2^{{t_1}}}{.2^{{t_2}}} = 64\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4m - 8 > 0\\{2^{{t_1} + {t_2}}} = 64\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4m - 8 > 0\\{t_1} + {t_2} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4m - 8 > 0\\m = 6\end{array} \right. \Leftrightarrow m = 6\).
Câu 31:
Cho hình lăng trụ tam giác đều \[ABC.A'B'C'.\] Góc giữa hai mặt phẳng \[\left( {A'BC} \right)\] và \[\left( {ABC} \right)\]bằng \[30^\circ .\] Tam giác \[A'BC\] có diện tích bằng 8. Tính thể tích khối lăng trụ \[ABC.A'B'C'.\]
 Xem đáp án
Xem đáp án
Đáp án A
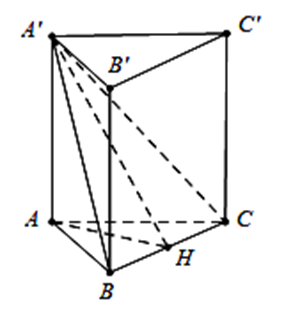
Kẻ \(AH \bot BC \Rightarrow \widehat {\left( {(A'BC);(ABC)} \right)} = \widehat {A'HA} = 30^\circ \)
\( \Rightarrow \cos 30^\circ = \frac{{AH}}{{A'H}} = \frac{{\sqrt 3 }}{2} \Rightarrow A'H = \frac{2}{{\sqrt 3 }}AH = \frac{2}{{\sqrt 3 }}.\frac{{AB\sqrt 3 }}{2} = AB\).
\({S_{A'BC}} = \frac{1}{2}BC.A'H = \frac{1}{2}AB.AB = 8 \Rightarrow AB = 4\).
\(\tan 30^\circ = \frac{{A'A}}{{AH}} = \frac{{A'A}}{{\frac{{AB\sqrt 3 }}{2}}} \Rightarrow A'A = 2\)
\( \Rightarrow V = A'A.{S_{ABC}} = A'A.\frac{{A{B^2}\sqrt 3 }}{4} = 8\sqrt 3 \).
Câu 32:
Trong không gian Oxyz, cho đường thẳng \[d:\frac{{x + 4}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 3}}{1}\] và hai điểm \[A\left( {1;0;1} \right),{\rm{ }}B\left( {2;1;0} \right).\] Mặt phẳng \[\left( Q \right):ax + by + cz - 4 = 0\] đi qua hai điểm A và B đồng thời song song với đường thẳng d. Tính \[a + b + c.\]
 Xem đáp án
Xem đáp án
Đáp án B
Đường thẳng d có một VTCP là \(\overrightarrow u = \left( {1; - 2;1} \right)\).
Mặt phẳng \(\left( Q \right)\) qua A, B và \(\left( Q \right){\rm{ // }}\left( P \right) \Rightarrow \left( Q \right)\) sẽ nhận \(\left[ {\overrightarrow {AB} ;\overrightarrow u } \right]\) là một VTPT.
Ta có \(\left\{ \begin{array}{l}\overrightarrow {AB} = \left( {1;1; - 1} \right)\\\overrightarrow u = \left( {1; - 2;1} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow u } \right] = \left( { - 1; - 2; - 3} \right) \Rightarrow \left( Q \right)\) sẽ nhận \(\overrightarrow {{n_Q}} = \left( {1;2;3} \right)\) là một VTPT.
Kết hợp với \(\left( Q \right)\) qua \(A\left( {1;0;1} \right) \Rightarrow 1.\left( {x - 1} \right) + 2\left( {y - 0} \right) + 3\left( {z - 1} \right) = 0\)
\( \Rightarrow \left( Q \right):x + 2y + 3{\rm{z}} - 4 = 0\).
Đường thẳng d qua \(M\left( { - 4;2; - 3} \right)\), rõ ràng \(M \notin \left( Q \right):x + 2y + 3{\rm{z}} - 4 = 0\)
\( \Rightarrow \left( Q \right):x + 2y + 3{\rm{z}} - 4 = 0\) thỏa mãn.
Câu 33:
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):2x - 5y - z = 0\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 3}}{{ - 1}}.\] Viết phương trình đường thẳng Δ nằm trên mặt phẳng (P) sao cho Δ cắt và vuông góc với đường thẳng d.
 Xem đáp án
Xem đáp án
Đáp án A
Ta có \(d:\left\{ \begin{array}{l}x = 1 + t\\y = - 1 + t\\z = 3 - t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\).
Giả sử \(\Delta \) cắt và vuông góc với d tại \(M \Rightarrow M\left( {t + 1;t - 1;3 - t} \right)\).
Bài ra \(\Delta \) nằm trên \(\left( P \right) \Rightarrow M \in \left( P \right) \Rightarrow 2\left( {t + 1} \right) - 5\left( {t - 1} \right) - \left( {3 - t} \right) = 0\)
\( \Leftrightarrow - 2t + 4 = 0 \Leftrightarrow t = 2 \Rightarrow M\left( {3;1;1} \right)\).
Mặt phẳng \(\left( P \right)\) có một VTPT là \(\overrightarrow n = \left( {2; - 5; - 1} \right)\).
Đường thẳng d có một VTCP là \(\overrightarrow u = \left( {1;1; - 1} \right)\).
Đường thẳng \(\Delta \) nằm trên \(\left( P \right)\) và \(\Delta \bot {\rm{d}} \Rightarrow \Delta \) nhận \(\left[ {\overrightarrow n ;\overrightarrow u } \right] = \left( {6;1;7} \right)\) là một VTCP.
Kết hợp với \(\Delta \) qua \(M\left( {3;1;1} \right) \Rightarrow \Delta :\frac{{x - 3}}{6} = \frac{{y - 1}}{1} = \frac{{z - 1}}{7}\).
Câu 34:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh \[SA = a\sqrt 3 \] và vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng \[\left( {SCD} \right)\] và \[\left( {ABCD} \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án D
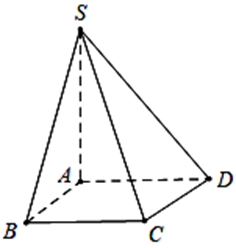
Ta có \(\left\{ \begin{array}{l}C{\rm{D}} \bot A{\rm{D}}\\C{\rm{D}} \bot {\rm{S}}A\end{array} \right. \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot {\rm{SD}}\).
Do đó \(\widehat {\left( {(SC{\rm{D}});(ABC{\rm{D}})} \right)} = \widehat {S{\rm{D}}A}\).
\[\tan \widehat {S{\rm{D}}A} = \frac{{SA}}{{A{\rm{D}}}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {S{\rm{D}}A} = 60^\circ \].
Câu 35:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Khoảng cách từ điểm A đến mặt phẳng \[\left( {SBC} \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án C
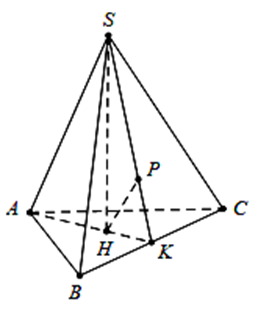
Kẻ \(SH \bot \left( {ABC} \right)\), gọi \(K = AH \cap BC\).
Kẻ \(HP \bot {\rm{S}}K \Rightarrow d\left( {A;(SBC)} \right) = \frac{3}{2}d\left( {H;(SBC)} \right) = \frac{3}{2}HP = d\).
Ta có \(\frac{1}{{H{P^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{K^2}}}\). Cạnh \(HK = \frac{{AB}}{{2\sqrt 3 }} = \frac{a}{{2\sqrt 3 }}\)
\(S{H^2} = S{A^2} - A{H^2} = 4{{\rm{a}}^2} - {\left( {\frac{{AB}}{{\sqrt 3 }}} \right)^2} = \frac{{11{{\rm{a}}^2}}}{3}\)
\( \Rightarrow HP = a\sqrt {\frac{{11}}{{135}}} \Rightarrow d\left( {A;(SBC)} \right) = \frac{{a\sqrt {165} }}{{15}}\).
Câu 36:
Cho hàm số \[y = f\left( x \right)\]. Hàm số \[y = f'\left( x \right)\] có bảng biến thiên như sau:
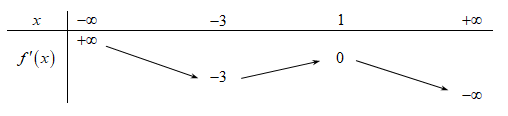
Bất phương trình \[f\left( x \right) < {x^3} + m\] đúng với mọi \[x \in \left( { - 2;1} \right)\] khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án C
Xét hàm số \(g\left( x \right) = f\left( x \right) - {x^3},x \in \left( { - 2;1} \right) \Rightarrow g'\left( x \right) = f'\left( x \right) - 3{{\rm{x}}^2}\).
Với mọi \(x \in \left( { - 2;1} \right)\) thì \(f'\left( x \right) < 0 \Rightarrow g'\left( x \right) < 0,\forall x \in \left( { - 2;1} \right)\)
\( \Rightarrow g\left( x \right)\) nghịch biến trên \(\left( { - 2;1} \right)\).
Khi đó \(m > g\left( x \right),\forall x \in \left( { - 2;1} \right) \Leftrightarrow m \ge g\left( { - 2} \right) \Leftrightarrow m \ge f\left( { - 2} \right) + 8\).
Câu 37:
Cho hàm số f(x) liên tục trên đoạn \[\left[ {0;{\mkern 1mu} 10} \right]\] thỏa mãn \[\int\limits_0^{10} {f\left( x \right){\rm{d}}x = 7} \] và \[\int\limits_2^6 {f\left( x \right){\rm{d}}x = 3} \]. Tính \[P = \int\limits_0^2 {f\left( x \right){\rm{d}}x + \int\limits_6^{10} {f\left( x \right){\rm{d}}x} } \].
 Xem đáp án
Xem đáp án
Đáp án C
Ta có \(\int\limits_0^{10} {f\left( x \right)d{\rm{x}}} = 7 \Leftrightarrow \int\limits_0^2 {f\left( x \right)d{\rm{x}}} + \int\limits_2^6 {f\left( x \right)d{\rm{x}}} + \int\limits_6^{10} {f\left( x \right)d{\rm{x}}} = 7\)
\( \Rightarrow P + \int\limits_2^6 {f\left( x \right)d{\rm{x}}} = 7 \Rightarrow P + 3 = 7 \Rightarrow P = 4\).
Câu 38:
Cho khối lăng trụ \[ABC.A'B'C'\] có thể tích bằng \[9{a^3}\] và M là điểm nằm trên cạnh \[CC'\] sao cho \[MC = 2MC'\]. Thể tích khối tứ diện \[AB'CM\] bằng
 Xem đáp án
Xem đáp án
Đáp án A
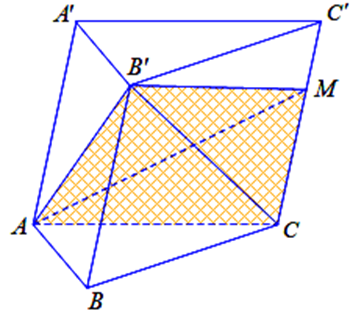
Ta có \({V_{AB'CM}} = {V_{B'.ACM}} = \frac{1}{3}d\left( {B';(ACM)} \right).{S_{ACM}}\).
Từ \(BB'{\rm{ // CM}} \Rightarrow {\rm{BB' // }}\left( {ACM} \right)\)
\( \Rightarrow d\left( {B';(ACM)} \right) = d\left( {B;(ACM)} \right)\)
\( \Rightarrow {V_{AB'CM}} = \frac{1}{3}d\left( {B;(ACM)} \right).{S_{ACM}} = {V_{B.ACM}} = {V_{M.ABC}}\)
\( = \frac{2}{3}{V_{C'.ABC}} = \frac{2}{3}.\frac{1}{3}{V_{ABC.A'B'C'}} = 2{{\rm{a}}^3}\).
Câu 39:
Có bao nhiêu số phức \[z\] thỏa mãn \[\left( {1 + i} \right)z + \bar z\] là số thuần ảo và \[\left| {z - 2i} \right| = 1\]?
 Xem đáp án
Xem đáp án
Đáp án A
Giả sử \(z = a + bi{\rm{ }}\left( {a,b \in \mathbb{R}} \right)\)
Ta có \(\left| {z - 2i} \right| = 1 \Leftrightarrow \left| {a + \left( {b - 2} \right)i} \right| = 1 \Leftrightarrow \sqrt {{a^2} + {{\left( {b - 2} \right)}^2}} = 1 \Leftrightarrow {a^2} + {\left( {b - 2} \right)^2} = 1.\)
Lại có \(\left( {1 + i} \right)z + \overline z = \left( {1 + i} \right)\left( {a + bi} \right) + a - bi = 2{\rm{a}} - b + ai\) là số thuần ảo.
Nên \(2a - b = 0 \Rightarrow b = 2a \Rightarrow {a^2} + {\left( {2a - 2} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}a = 1\\a = \frac{3}{5}\end{array} \right.\)
+ Với \(a = 1 \Rightarrow b = 2 \Rightarrow z = 1 + 2i\).
+ Với \(a = \frac{3}{5} \Rightarrow b = \frac{6}{5} \Rightarrow z = \frac{3}{5} + \frac{6}{5}i\).
Câu 40:
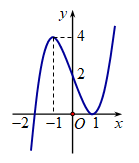
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Số nghiệm thực của phương trình \[f\left( {{f^2}\left( x \right) - 3} \right) = 0\] là
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \(f\left( {{f^2}(x) - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{f^2}\left( x \right) - 3 = - 2\\{f^2}\left( x \right) - 3 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 1\\f\left( x \right) = - 1\\f\left( x \right) = 2\\f\left( x \right) = - 2\end{array} \right.\).
\(f\left( x \right) = 1\) có đúng 3 nghiệm phân biệt; \(f\left( x \right) = - 1\) có đúng 1 nghiệm.
\(f\left( x \right) = 2\) có đúng 3 nghiệm phân biệt; \(f\left( x \right) = - 2\) có đúng 1 nghiệm.
Các nghiệm nói trên không trùng nhau.
Câu 41:
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x + y - z - 3 = 0\] và hai điểm \[A\left( {1;1;1} \right)\], \[B\left( { - 3; - 3; - 3} \right)\]. Mặt cầu \[\left( S \right)\] đi qua hai điểm \[A,{\rm{ }}B\] và tiếp xúc với (P) tại điểm C. Biết rằng C luôn thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó
 Xem đáp án
Xem đáp án
Đáp án B
Gọi \(I = AB \cap \left( P \right)\).
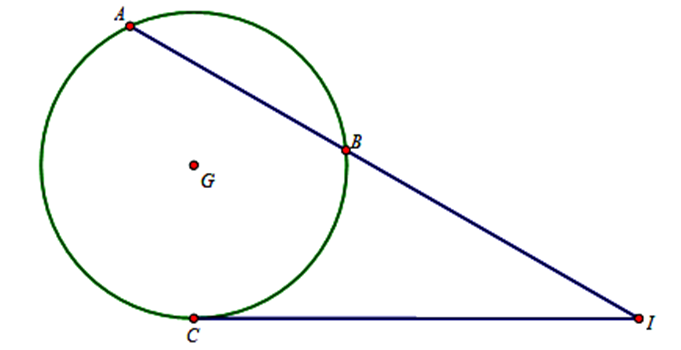
Ta có \(\overrightarrow {BA} = \left( {4;4;4} \right) = 4\left( {1;1;1} \right) \Rightarrow AB:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + t\\z = 1 + t\end{array} \right. \Rightarrow I\left( {t + 1;t + 1;t + 1} \right).\)
Mà \(I \in \left( P \right) \Rightarrow \left( {t + 1} \right) + \left( {t + 1} \right) - \left( {t + 1} \right) - 3 = 0 \Leftrightarrow t = 2 \Rightarrow I\left( {3;3;3} \right)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {IA} = \left( { - 2; - 2; - 2} \right)}\\{\overrightarrow {IB} = \left( { - 6; - 6; - 6} \right)}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{IA = 2\sqrt 3 }\\{IB = 6\sqrt 3 }\end{array}} \right.\)
Mặt cầu \(\left( S \right)\) tiếp xúc với \(\left( P \right)\) tại C nên IC là tiếp tuyến của \(\left( S \right)\).
Do đó \(IA.IB = I{C^2} \Rightarrow IC = \sqrt {IA.IB} = 6 \Rightarrow C\) thuộc mặt cầu có tâm \(I\left( {3;3;3} \right)\) và bán kính \(R = IC = 6\).
Câu 42:
Cho hình nón (N) có đường sinh bằng a, góc ở đỉnh bằng \[90^\circ .\] Thiết diện qua đỉnh của (N) là một tam giác nằm trong mặt phẳng tạo với mặt phẳng đáy một góc bằng \[60^\circ .\] Tính theo a diện tích S của tam giác này.
 Xem đáp án
Xem đáp án
Đáp án A
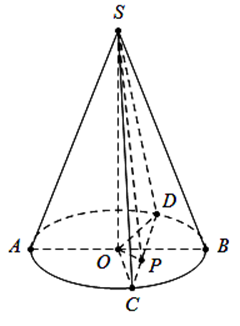
\(\Delta SAB\) vuông cân tại \(S \Rightarrow SO = OA = OB = \frac{a}{{\sqrt 2 }}\).
Thiết diện qua đỉnh của \(\left( N \right)\) là \(\Delta SC{\rm{D}}\) như hình vẽ.
Kẻ \(OP \bot C{\rm{D}} \Rightarrow \widehat {\left( {(SC{\rm{D}});(OC{\rm{D}})} \right)} = \widehat {SPO} = 60^\circ \).
\(\sin 60^\circ = \frac{{SO}}{{SP}} = \frac{{\sqrt 3 }}{2} \Rightarrow SP = \frac{2}{{\sqrt 3 }}.SO = \frac{2}{{\sqrt 3 }}.\frac{a}{{\sqrt 2 }} = a\sqrt {\frac{2}{3}} \).
\(\tan 60^\circ = \frac{{SO}}{{OP}} \Rightarrow OP = \frac{{SO}}{{\sqrt 3 }} = \frac{a}{{\sqrt 6 }}\)
\( \Rightarrow P{\rm{D}} = \sqrt {O{{\rm{D}}^2} - O{P^2}} = \sqrt {{{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2} - {{\left( {\frac{a}{{\sqrt 6 }}} \right)}^2}} = \frac{a}{{\sqrt 3 }}\)
\( \Rightarrow C{\rm{D}} = 2P{\rm{D}} = \frac{{2{\rm{a}}}}{{\sqrt 3 }} \Rightarrow {S_{SC{\rm{D}}}} = \frac{1}{2}SP.C{\rm{D}} = \frac{{{a^2}\sqrt 2 }}{3}\).
Câu 43:
Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.
 Xem đáp án
Xem đáp án
Đáp án D
Rút ngẫu nhiên 10 tấm thẻ từ 40 tấm thẻ có \(C_{40}^{10}\) cách.
Từ số 1 đến số 40 có 6 số chia hết cho 6 là 6; 12; 18; …36, đặt \(M = \left\{ {6;12;18;...36} \right\}\).
Chọn 1 số chia hết cho 6 từ tập M có \(C_6^1\) cách (số được chọn là số chẵn).
Rút 4 số chẵn (cho đủ 5 số chẵn) từ tập \(K = \left\{ {2;4;...40} \right\}\backslash M\) có \(C_{20 - 6}^4 = C_{14}^4\) cách.
Rút 5 số lẻ có \(C_{20}^5\) cách.
Vậy xác suất cần tìm là \(\frac{{C_6^1.C_{14}^4.C_{20}^5}}{{C_{40}^{10}}} = \frac{{126}}{{1147}}\).
Câu 44:
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\left[ {0;1} \right]\] thỏa mãn \[f'\left( x \right) = \left( {2x + 1} \right){e^x} + f\left( x \right)\] và \[f\left( 0 \right) = 0.\] Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Ta có \(\frac{{f'\left( x \right) - f\left( x \right)}}{{{e^x}}} = 2{\rm{x}} + 1 \Rightarrow \frac{{f'\left( x \right).{e^x} - f\left( x \right).{e^x}}}{{{{\left( {{e^x}} \right)}^2}}} = 2{\rm{x}} + 1\)
\( \Rightarrow {\left[ {\frac{{f\left( x \right)}}{{{e^x}}}} \right]^\prime } = 2{\rm{x}} + 1 \Rightarrow \frac{{f\left( x \right)}}{{{e^x}}} = \int {\left( {2{\rm{x}} + 1} \right)d{\rm{x}}} = {x^2} + x + C\).
Mà \(f\left( 0 \right) = 0 \Rightarrow C = 0 \Rightarrow f\left( x \right) = \left( {{x^2} + x} \right){e^x} \Rightarrow f\left( 1 \right) = 2{\rm{e}}\).
Câu 45:
Cho hàm số f(x) có đạo hàm \[f'\left( x \right) = {\left( {x - 1} \right)^3}{\left( {x + 3} \right)^5}\left( {x + 1} \right)g\left( x \right) - \frac{2}{{\sqrt {{x^2} - 2x + 5} }},\forall x \in \mathbb{R}.\] Trong đó \[g\left( x \right) > 0\], \[\forall x \in \mathbb{R}.\] Hàm số \[y = f\left( {2x + 1} \right) + \ln \left( {x + \sqrt {{x^2} + 1} } \right)\] nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án D
Ta có \(y' = 2f'\left( {2x + 1} \right) + \frac{1}{{x + \sqrt {{x^2} + 1} }}.\left( {1 + \frac{x}{{\sqrt {{x^2} + 1} }}} \right)\)
\( = 2{\left( {2x} \right)^3}{\left( {2x + 4} \right)^5}\left( {2x + 2} \right)g\left( {2x + 1} \right) - \frac{2}{{\sqrt {{{\left( {2x + 1} \right)}^2} - 2\left( {2x + 1} \right) + 5} }} + \frac{1}{{\sqrt {{x^2} + 1} }}\)
\( = 2{\left( {2x} \right)^3}{\left( {2x + 4} \right)^5}\left( {2x + 2} \right)g\left( {2x + 1} \right) - \frac{2}{{\sqrt {4{x^2} + 4} }} + \frac{1}{{\sqrt {{x^2} + 1} }} < 0\)
\( = 2{\left( {2x} \right)^3}{\left( {2x + 4} \right)^5}\left( {2x + 2} \right) < 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x < - 2}\\{ - 1 < x < 0}\end{array}} \right..\)
Câu 46:
Cho \[a,{\rm{ }}b\] là các số thực dương thỏa mãn \[b > 1\] và \[\sqrt a \le b < a.\] Giá trị nhỏ nhất của biểu thức \[P = {\log _{\frac{a}{b}}}a + 2{\log _{\sqrt b }}\left( {\frac{a}{b}} \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án C
Ta có \(P = \frac{1}{{{{\log }_a}\frac{a}{b}}} + 4{\log _b}\frac{a}{b} = \frac{1}{{1 - {{\log }_a}b}} + 4\left( {{{\log }_b}a - 1} \right) = \frac{1}{{1 - {{\log }_a}b}} + \frac{4}{{{{\log }_a}b}} - 4.\)
Đặt \(t = {\log _a}b \Rightarrow P = \frac{1}{{1 - t}} + \frac{4}{t} - 4.\)
Từ \(a > \sqrt a \Rightarrow a > 1 \Rightarrow t = {\log _a}b < {\log _a}a \Rightarrow t < 1.\)
Từ \(b \ge \sqrt a \Rightarrow t = {\log _a}b \ge {\log _a}\sqrt a = \frac{1}{2} \Rightarrow \frac{1}{2} \le t < 1.\)
Xét hàm số \(f\left( t \right) = \frac{1}{{1 - t}} + \frac{4}{t} - 4\), với \(t \in \left[ {\frac{1}{2};1} \right)\) có \(\left\{ {\begin{array}{*{20}{l}}{t \in \left( {\frac{1}{2};1} \right)}\\{f'\left( t \right) = \frac{1}{{{{\left( {1 - t} \right)}^2}}} - \frac{4}{{{t^2}}} = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t \in \left( {\frac{1}{2};1} \right)}\\{t = 2\left( {1 - t} \right)}\end{array}} \right. \Leftrightarrow t = \frac{2}{3}.\)
Xét bảng sau:
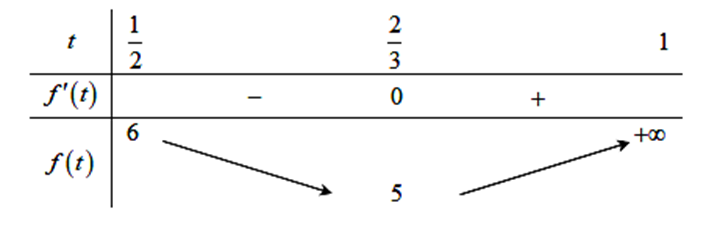
Từ đó \(\mathop {\min }\limits_{\left[ {\frac{1}{2};1} \right)} f\left( t \right) = 5\).
Câu 47:
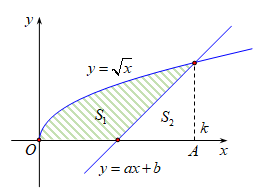
Cho hình phẳng (H) giới hạn bởi các đường \[y = \sqrt x ,{\rm{ }}y = 0,{\rm{ }}x = k{\rm{ }}\left( {k > 0} \right).\] Đường thẳng \[y = ax + b\] đi qua trung điểm của đoạn thẳng OA và chia (H) thành hai phần có diện tích \[{S_1}\], \[{S_2}\] như hình vẽ. Biết \[3{S_1} + {S_2} = 12,\] tính \[a + b.\]
 Xem đáp án
Xem đáp án
Đáp án C
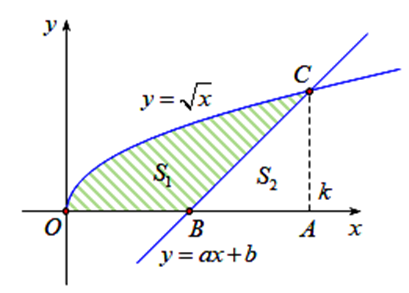
Ta có: \({S_1} + {S_2} = \int\limits_0^k {\sqrt x dx} = \int\limits_0^{\sqrt k } {td\left( {{t^2}} \right)} = \int\limits_0^{\sqrt k } {t.2tdt} = \frac{{2k\sqrt k }}{3}.\)
\({S_2} = \frac{1}{2}AC.AB = \frac{1}{2}\sqrt k .\frac{k}{2} = \frac{1}{4}k\sqrt k \)
\( \Rightarrow {S_1} = \frac{2}{3}k\sqrt k - \frac{1}{4}k\sqrt k = \frac{5}{{12}}k\sqrt k \)
\( \Rightarrow 3{S_1} + {S_2} = \frac{3}{2}k\sqrt k = 12 \Rightarrow k = 4.\)
Đường thẳng \(y = ax + b\) qua
\(B\left( {2;0} \right),C\left( {4;2} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2a + b = 0}\\{4a + b = 2}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 2}\end{array}} \right..\)
Câu 48:
Trong không gian Oxyz, cho mặt \[\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y + 4z = 0\] và điểm \[M\left( {1;2; - 1} \right).\] Một đường thẳng thay đổi qua M và cắt \[\left( S \right)\] tại hai điểm phân biệt \[A,{\rm{ }}B.\] Tìm giá trị lớn nhất của tổng \[MA + MB.\]
 Xem đáp án
Xem đáp án
Đáp án C
Mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 2} \right)^2} = 9\) có tâm \(I\left( {1; - 2; - 2} \right)\), bán kính \(R = 3\).
Gọi d là đường thẳng thay đổi qua M và cắt \(\left( S \right)\) tại hai điểm phân biệt A, B.
Ta có \(\overrightarrow {MI} = \left( {0; - 4; - 1} \right) \Rightarrow MI = \sqrt {17} > R \Rightarrow M\) nằm ngoài \(\left( S \right)\).
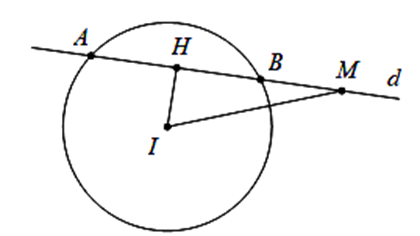
Gọi H là trung điểm của cạnh AB.
Ta có \(MA + MB = \left( {MH + HA} \right) + MB = MH + HB + MB = MH + HM = 2MH \le 2MI = 2\sqrt {17} .\)
Dấu “=” xảy ra \( \Leftrightarrow d\) qua I.
Câu 49:
Cho phương trình \[2\sqrt {m + x} - \sqrt {m - x} = \sqrt {m - x + \sqrt {x\left( {m + x} \right)} } \] (m là tham số thực) có tổng các nghiệm thực bằng \[\frac{{192}}{{205}}.\] Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Điều kiện \(\left\{ \begin{array}{l}m + x \ge 0\\m - x \ge 0\\x \ge 0\end{array} \right. \Rightarrow \left( {m + x} \right) + \left( {m - x} \right) \ge 0 \Rightarrow m \ge 0.\)
Ta thấy \(x = 0\) thỏa mãn phương trình.
Với \(x > 0 \Rightarrow 2\sqrt {\frac{m}{x} + 1} - \sqrt {\frac{m}{x} - 1} = \sqrt {\frac{m}{x} - 1 + \sqrt {\frac{m}{x} + 1} } .\)
Đặt \(t = \frac{m}{x} \ge 0 \Rightarrow 2\sqrt {t + 1} - \sqrt {t - 1} = \sqrt {t - 1 + \sqrt {t + 1} } \)
\( \Rightarrow 4\left( {t + 1} \right) + \left( {t - 1} \right) - 4\sqrt {{t^2} - 1} = t - 1 + \sqrt {t + 1} \)
\( \Rightarrow 4\left( {t + 1} \right) - 4\sqrt {\left( {t + 1} \right)\left( {t - 1} \right)} = \sqrt {t + 1} \)
\( \Rightarrow 4\sqrt {t + 1} - 4\sqrt {t - 1} = 1 \Rightarrow 16\left( {t + 1} \right) = 16\left( {t - 1} \right) + 1 + 8\sqrt {t - 1} \Rightarrow 8\sqrt {t - 1} = 31 \Rightarrow t = \frac{{1025}}{{64}}.\)
Thử lại ta thấy thỏa mãn \( \Rightarrow \frac{m}{x} = \frac{{1025}}{{64}} \Rightarrow x = \frac{{64m}}{{1025}} \Rightarrow 0 + \frac{{64m}}{{1025}} = \frac{{192}}{{205}} \Rightarrow m = 15.\)
Câu 50:
Cho ba số phức \[{z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}\] thỏa mãn \[\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1\]; \[\left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\] và \[z_1^2 = {z_2}{z_3}.\] Tính giá trị của \[\left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right|\].
 Xem đáp án
Xem đáp án
Đáp án D
Gọi M, N, P lần lượt là các điểm biểu diễn các số phức \({z_1},{z_2},{z_3}\).
Suy ra M, N, P thuộc đường tròn \(\left( {O;1} \right)\).
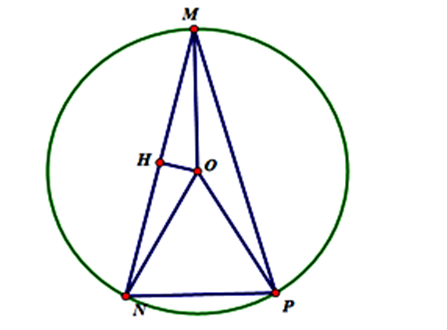
Ta có \(MN = \left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\).
Kẻ \(OH \bot MN \Rightarrow MH = \frac{{MN}}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4} \Rightarrow \cos \widehat {OMN} = \frac{{MN}}{{OM}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\( \Rightarrow \widehat {OMN} = {15^0} \Rightarrow \widehat {MON} = {150^0}\)
Ta có \(\left| {{z_3} - {z_1}} \right| = \left| {{z_1}} \right|.\left| {{z_3} - {z_1}} \right| = \left| {{z_3}{z_1} - z_1^2} \right| = \left| {{z_3}{z_1} - {z_3}{z_2}} \right| = \left| {{z_3}} \right|.\left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\)
\( \Rightarrow MP = \left| {{z_3} - {z_1}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2} \Rightarrow MN = MP = \frac{{\sqrt 6 + \sqrt 2 }}{2}.\)
Tương tự như trên \( \Rightarrow \widehat {MOP} = {150^0} \Rightarrow \widehat {NOP} = {360^0} - \left( {{{150}^0} + {{150}^0}} \right) = {60^0}\)
\( \Rightarrow \Delta NOP\) đều \( \Rightarrow NP = 1\)
\( \Rightarrow \left| {{z_2} - {z_3}} \right| = NP = 1 \Rightarrow \left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right| = 1 - \frac{{\sqrt 6 + \sqrt 2 }}{2} = \frac{{2 - \sqrt 6 - \sqrt 2 }}{2}.\)
