Cho hình chóp S.ABC có đường cao tam giác là tam giác cân tại A có AB=a,BAC=120°. Biết thể tích khối chóp S.ABC bằng √3a34, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
Giải bởi Vietjack
Đáp án D
Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:
+ Xác định giao tuyến d của (P) và (Q)
+ Trong mặt phẳng (P) xác định đường thẳng a⊥d , trong mặt phẳng (Q) xác định đường thẳng b⊥d .
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b.
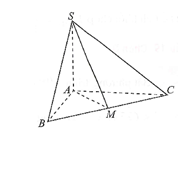
Gọi M là trung điểm BC (do ΔABC cân tại A).
Lại có ΔSAB=ΔSAC(c.g.c)⇒SB=SC hay ΔSBC cân tại S.
⇒SM⊥BC
Ta có {(SBC)∩(ABC)=BCAM⊥BC;AM⊂(ABC)SM⊥BC;SM⊂(SBC)
⇒⌢((SBC),(ABC))=(^SM,AM)=^SMA.
Theo đề bài VS.ABC=√3a324⇒13SA.SABC=a3√324⇔SA=a3√38:a2√34=a2 .
Lại thấy ΔABM vuông tại M có AB=a;^ABM=180°−^BAC2=30°
Xét tam giác SA=AM=a2 vuông tại có AB=a;^ABM=180°−^BAC2=30° nên ΔSAM vuông cân tại hay ^SMA=45°
Vậy góc giữa (SBC) và (ABC) là 45° .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10;10] để hàm số y=x3−3x2+3mx+2019 nghịch biến trên khoảng (1;2)?
Có tất cả bao nhiêu giá trị khác nhau của tham số m để đồ thị hàm số y=x−1x2+mx+4 có 2 đường tiệm cận?
Trong không gian , mặt phẳng đi qua điểm A(−1;−1;2) và song song với hai đường thẳng Δ:x−12=y+12=z−31,Δ' có phương trình là:
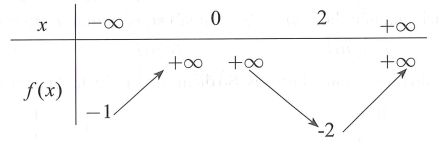
Tập hợp tất cả các giá trị thực của tham số m để phương trình có hai nghiệm phân biệt là
