Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân có . Cạnh bên SA vuông góc với đáy, . Gọi M là điểm nằm trên AC sao cho . Tính khoảng cách giữa SM và AB.
B.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
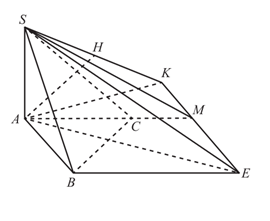
Trong (ABC), qua M kẻ đường thẳng song song với AB, qua B kẻ đường thẳng song song với AM. Hai đường thẳng này cắt nhau tại E ta được tứ giác ABEM là hình bình hành.
Vì
Từ A trong mặt phẳng (ABEM) kẻ , lại có: (do ).
Trong kẻ tại H.
Ta có (do )
tại H.
Từ đó .
Xét tam giác SBA vuông tại A có .
Lại có tam giác ABC vuông cân tại B nên .
Do đó .
vuông cân tại B nên (hai góc so le trong).
Từ đó , suy ra (hai góc đổi hình bình hành).
Nên tam giác AME là tam giác tù nên K nằm ngoài đoạn ME.
Ta có: mà tam giác AMK vuông tại K nên tam giác AMK vuông cân tại K.
Xét tam giác SAK vuông tại A có đường cao AH, ta có: .
Vậy
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAC) tạo với (SBC) một góc 60 độ và mặt phẳng (SAC) tạo với (SBC) một góc thỏa mãn . Gọi là góc tạo bởi SA và mặt phẳng (ABC) . Tính .
Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a. Hai mặt bên và cùng vuông góc với đáy và . Tính thể tích khối chóp S.ABC.
Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích của khối trụ là .
Cho hàm số . Với giá trị nào của m thì hai đường tiệm cận của đồ thị hàm số cùng với hai trục tọa độ tạo thành hình vuông.
Cho hàm số với m là tham số thực. Biết rằng hàm số có số điểm cực trị lớn hơn 5 khi . Giá trị bằng: