Cho các số thực dương a, b thỏa mãn điều kiện ${\log }_{3}a={\log }_{4}b={\log }_{12}\left(a^2-6b^2\right).$   Giá trị của biểu thức $P=\frac{a}{b}$  là

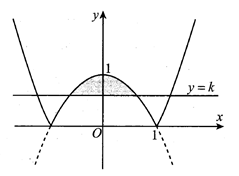
Cho hình phẳng (H) giới hạn bởi các đường $y=\left|x^2-1\right|$  và $y=k,\left(0<k<1\right).$  Tìm k để diện tích của hình phẳng  gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên.

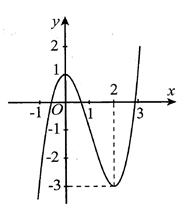
Cho hàm số y =f(x) có đồ thị là đường cong như hình vẽ. Khẳng định nào sau đây sai?

Tìm đạo hàm của hàm số  $f\left(x\right)={\log }_2\left(x+1\right).$

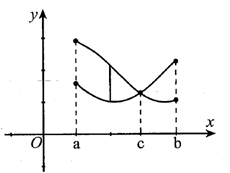
Tìm công thức tính diện tích S của hình phẳng (H) giới hạn bởi các đồ thị hàm số $y=f\left(x\right),y=g\left(x\right)$  và hai đường thẳng $x=a,x=b$   như hình vẽ. Biết rằng $f\left(x\right)\ge g\left(x\right),\forall x\in \left[a;c\right]$  và $f\left(x\right)\le g\left(x\right),\forall x\in \left[c;b\right].$   Khẳng định nào sau đây là đúng?

Gọi $z_1,z_2$  là nghiệm phức của phương trình $z^2+2z+10=0.$  Giá trị của biểu thức ${\left|z_1\right|}^2+{\left|z_2\right|}^2$  bằng

Cho mặt cầu (S) có bán kính R=5(cm) Mặt phẳng (P)   cắt mặt cầu (S) theo giao tuyến là đường tròn  có chu vi bằng $8\pi \left(cm\right).$  Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn(C)  ) và tam giác ABC là tam giác đều. Thể tích lớn nhất của tứ diện ABCD bằng

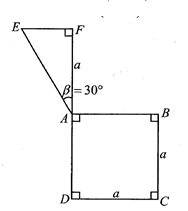
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF bằng

Có bao nhiêu số phức z thỏa mãn điều kiện  $2\left|z-i\right|=\left|z-\overline{z}+2i\right|$ và $\left|z^2+{\left(\overline{z}\right)}^2\right|=8$ ?

Gọi $z_1$  là nghiệm phức có phần ảo âm của phương trình $z^2+2z+3=0.$  Tọa độ điểm M biểu diễn số phức $z_1$  là

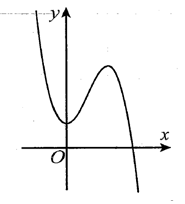
Cho hàm số $y=a{x}^3+b{x}^2+cx+d$  có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?

Gieo ngẫu nhiên 2 con xúc xắc cân đối đồng chất. Số phần tử của biến cố: “Hiệu số chấm xuất hiện trên 2 con xúc xắc bằng 1” là

Cho số phức z thỏa mãn $\left|z+3-4i\right|=5.$  Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính R của đường tròn đó.

Tìm m để đồ thị hàm số $y=\frac{m{x}^3-8}{x^2-3x+2}$  có hai đường tiệm cận đứng.