Cho hai điểm và mặt cầu (S) có phương trình . Viết phương trình mặt phẳng (P) đi qua A và tiếp xúc với sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử là một véctơ pháp tuyến của (P). Giá trị m+n bằng
A. 1
B. 2
D. 4
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho parabol và một đường thẳng d thay đổi cắt tại hai điểm A, B sao cho AB=2018 . Giá trị lớn nhất của diện tích hình phẳng giới hạn bởi (P) và đường thẳng d là
Cho mặt cầu (S) tâm O, bán kính R=3 . Một mặt phẳng cắt (S) theo giao tuyến là đường tròn (C) sao cho khoảng cách từ điểm O đến (C) bằng 1. Chu vi của đường tròn (C) bằng
Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là
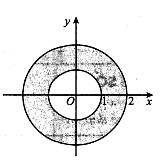
Tập hợp các điểm biểu diễn số phức , là miền tô đậm trong hình vẽ bên (kể cả biên). Kết luận nào sau đây đúng?
Cho đường thẳng . Gọi (P) là mặt phẳng vuông góc với Δ. Véctơ pháp tuyến của (P) là
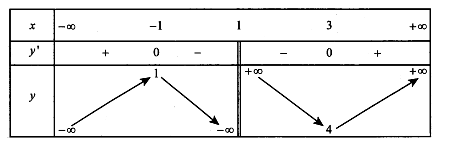
Khẳng định nào sau đây sai?