Trong không gian Oxyz, cho điểm ; mặt phẳng: : và mặt cầu (s): . Phương trình đường thẳng đi qua M và nằm trong cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất là
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Mặt cầu(S) có tâm I(2;3;4) và có bán kính R=4.
M nằm trong mặt cầu (S).
Để cắt mặt cầu theo một đoạn thẳng có độ dài thì khoảng cách từ I đến lớn nhất. Khi đó .
Gọi vectơ chỉ phương của là ta có
Đường thẳng qua và có vectơ chỉ phương là
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tất cả các giá trị thực của tham số m để hàm số đạt cực tiểu tại điểm là
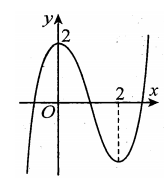
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số điểm cực trị của hàm số là
Biết hàm số f(x) thoả mãn các điều kiện f'(x)=2x+3 và f(0)=1. Giá trị f(2) là
Trong mặt phẳng phức với hệ tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện là