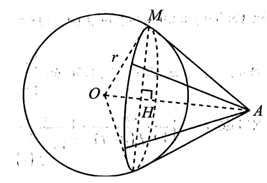
Trong không gian Oxyz, cho điểm M(1;-3;2). Có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại A, B, C thỏa mãn ?
A. 1
B. 2
C. 3
D. 4
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Gọi H là hình chiếu vuông góc của M lên OA.
Xét tam giác OMA vuông tại M có:
không đổi và H cố định.
Vậy M thuộc đường tròn .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp đều S.ABCD có thể tích bằng 1/3, đáy ABCD là hình vuông cạnh là 1. Phương trình mặt phẳng (ABCD) biết S(0;0;0) và là
Trong không gian Oxyz, cho mặt cầu và hai điểm . Gọi E là điểm thuộc mặt cầu(S) sao cho EM+EN đạt giá trị lớn nhất. Phương trình tiếp diện của mặt cầu (S) tại E là
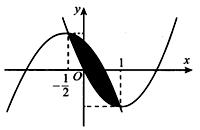
Miền phẳng trong hình vẽ giới hạn bởi y=f(x) và parabol . Biết . Khi đó diện tích hình phẳng được tô trong hình vẽ bằng
Cho hàm số y=f(x) liên tục, có đạo hàm trên [-5;3] và có bảng biến thiên sau.
![Cho hàm số y=f(x) liên tục, có đạo hàm trên [-5;3] và có bảng biến thiên sau. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/blobid2-1653234445.png)
Có bao nhiêu giá trị nguyên của m để phương trình có đúng 3 nghiệm thuộc ?
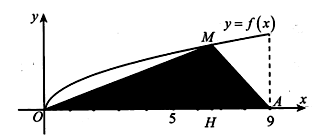
Cho đồ thị . Gọi (H) là hình phẳng giới hạn bởi đồ thị (C), đường thẳng x=9 và trục Ox. Cho điểm M thuộc đồ thị (C) và điểm A(9;0). Gọi là thể tích khối tròn xoay khi cho (H) quay quanh trục Ox, là thể tích khối tròn xoay khi cho tam giác AOM quay quanh trục Ox. Biết rằng . Tính diện tích S phần hình phẳng giới hạn bởi đồ thị (C) và đường thẳng OM.
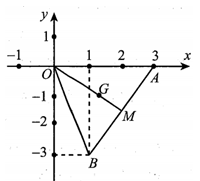
Trong A, B lần lượt là diểm biểu diễn các số phức . Trọng tâm G của tam giác OAB là điểm biểu diễn số phức như trong hình vẽ. Giá trị bằng:
Trong không gian Oxyz, cho hai mặt phẳng và . Các điểm A, B phân biệt cùng thuộc giao tuyến của hai mặt phẳng (P) và (Q). Khi đó cùng phương với vectơ nào sau đây?
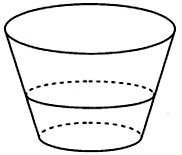
Một chậu nước hình nón cụt có chiều cao 3dm, bán kính đáy lớn là 2dm và bán kính đáy nhỏ là 1dm. Cho biết thể tích nước bằng thể tích của chậu, chiều cao của mực nước là
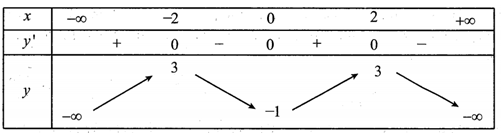
Cho hàm số có bảng biến thiên như sau:
Số điểm cực đại của hàm số đã cho bằng:
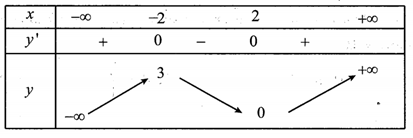
Đồ thị hàm số có bao nhiêu tiệm cận đứng?