Cho hình lăng trụ đứng \(ABC.A'B'C'\) có \(AB = AC = a,\) góc \(BAC = {120^0},AA' = a.\) Gọi \(M,N\) lần lượt là trung điểm của \(B'C'\) và \(CC'.\) Số đo góc giữa mặt phẳng \(\left( {AMN} \right)\) và mặt phẳng \(\left( {ABC} \right)\) bằng
A.\({60^0}.\)
B.\({30^0}.\)
C.\(\arccos \frac{{\sqrt 3 }}{4}.\)
D. \[\arcsin \frac{{\sqrt 3 }}{4}.\]
Giải bởi Vietjack
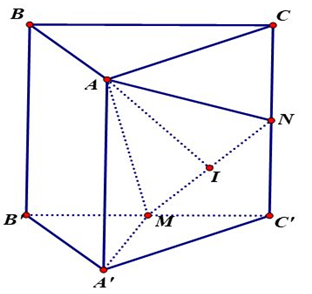
Ta có \(\Delta A'MC'\) vuông tại \(M\) có \(\widehat {A'C'M} = {30^0} \Rightarrow A'M = \frac{1}{2}.A'C' = \frac{2}{2}\)
\(MC' = \frac{{a\sqrt 3 }}{2} \Rightarrow B'C' = a\sqrt 3 .\)
Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {AMN} \right)\) và mặt phẳng \(\left( {ABC} \right) \Rightarrow \alpha = \left( {\widehat {\left( {AMN} \right);\left( {A'B'C'} \right)}} \right)\)
Tam giác \(A'MC'\) là hình chiếu của tam giác AMN trên mặt phẳng \(\left( {A'B'C'} \right)\) nên \(\cos \alpha = \frac{{{S_{A'MC'}}}}{{{S_{AMN}}}}\)
Ta có \({S_{A'MC'}} = \frac{1}{2}.{S_{ABC}} = \frac{1}{4}.AB.AC.\sin \widehat {BAC} = \frac{{\sqrt 3 {a^2}}}{8}.\)
\(A{N^2} = A{C^2} + C{N^2} = {a^2} + {\left( {\frac{a}{2}} \right)^2} = \frac{{5{a^2}}}{4} \Rightarrow AN = \frac{{a\sqrt 5 }}{2}.\)
\(M{N^2} = C'{N^2} + C'{M^2} = \frac{{{a^2}}}{4} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} \Rightarrow MN = a.\)
Gọi \[I\] là trung điểm của \(MN \Rightarrow AI \bot MN\)
\(AI = \sqrt {A{N^2} - I{N^2}} = a\)
\({S_{AMN}} = \frac{1}{2}.AI.MN = \frac{{{a^2}}}{2} \Rightarrow \cos \alpha = \frac{{\sqrt 3 }}{4}\)
Vậy số đo góc giữa mặt phẳng \(\left( {AMN} \right)\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(\arccos \frac{{\sqrt 3 }}{4}.\)
Đáp án C
Gói VIP thi online tại VietJack (chỉ 200k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right)x + 2\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\) Số phần tử của \(S\) bằng
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f\left( x \right) = 3\) là
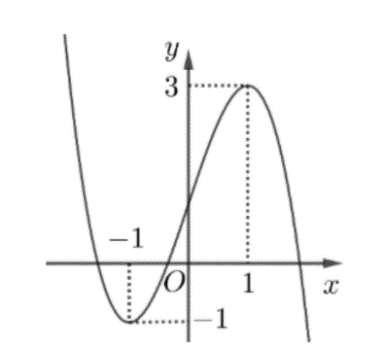
Cho hàm số có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số \(a,b,c,d?\)
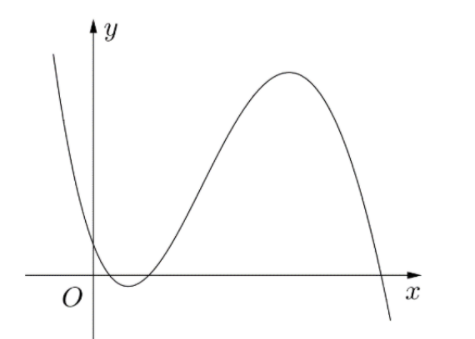
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = {x^3} + 3{x^2} - 3\) song song với trục hoành?
Cho hàm số \(y = {x^3} + 3{x^2} + 1\) có đồ thị \(\left( C \right)\) và điểm \(A\left( {1;m} \right).\) Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để qua A có thể kể được đúng ba tiếp tuyến tới đồ thị \(\left( C \right).\) Số phần tử của \(S\) là
Giá trị lớn nhất của hàm số \(y = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn \(\left[ { - 1;2} \right]\) là
Cho một đa giác đều có 18 đỉnh nội tiếp đường tròn tâm \(O.\) Gọi \(X\) là tập hợp tất cả các tam giác có 3 đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho. Chọn 1 tam giác trong tập hợp \(X.\) Xác suất để tam giác được chọn là tam giác cân bằng
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của đạo hàm
Hàm số đồng biến trên khoảng nào dưới đây?
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong \(t\) giờ được cho bởi công thức \(c\left( t \right) = \frac{t}{{{t^2} + 1}}\left( {mg/L} \right).\) Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Góc giữa đường thẳng \(SB\) và mặt phẳng đáy bằng.
Giá trị của biểu thức \(A = {2^{{{\log }_4}9 + {{\log }_2}5}}\) là
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a,\) cạnh bên SA vuông góc với mặt phẳng đáy và \(SA = a\sqrt 2 .\) Thể tích của khối chóp \(S.ABCD\) bằng
Với các số thực dương \(a,b\) bất kì. Mệnh đề nào dưới đây đúng?
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\left( {a \ne 0} \right)\) có đồ thị của đạo hàm \(f'\left( x \right)\) như hình vẽ. Biết rằng \(e >n.\)
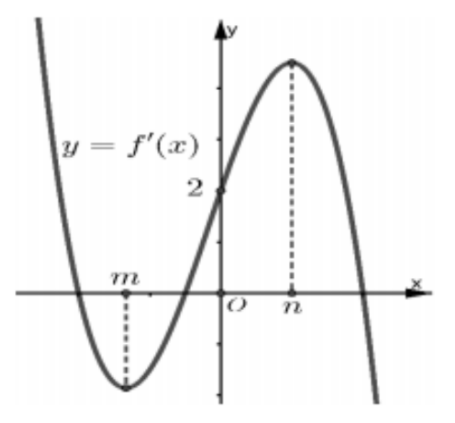
Số điểm cực trị của hàm số \(y = f'\left( {f\left( x \right) - 2x} \right)\) là
