Cho lăng trụ đứng ABC.A′B′C′ có độ dài cạnh bên là 2a, đáy ABC là tam giác vuông cân tại A, góc giữa AC′ và mặt phẳng (BCC′B′) bằng 300 (tham khảo hình vẽ).
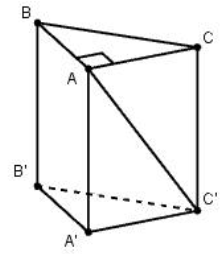
Tính theo a thể tích khối trụ có hai đáy là hai đường tròn ngoại tiếp hai đáy của lăng trụ ABC.A′B′C′.
A.πa3.
B. 3πa3.
C.2πa3.
D.4πa3.
 Giải bởi Vietjack
Giải bởi Vietjack
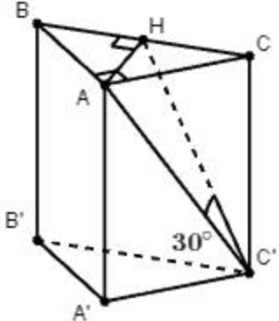
Gọi H là trung điểm của đoạn BC, vì ΔABC là tam giác vuông cân nên H là chân đường cao xuất phát từ đỉnh A đồng thời cũng là tâm đường tròn ngoại tiếp ΔABC.
Suy ra bán kính đường tròn ngoại tiếp đáy của lăng trụ ABC.A′B′C′ là HC.
Vì {AH⊥BCAH⊥BB′ nên AH⊥(BCC′B′).
Suy ra HC là hình chiếu vuông góc của AC lên (BCC′B′).
Góc giữa AC′ và mặt phẳng (BCC′B′) là ^AC′H=300.
Đặt HC=x⇒AC=x√2.
Áp dụng định lý Pytago trong ΔACC′ ta được AC′=√2x2+4a2.
Áp dụng định lý Pytago trong ΔHCC′ ta được HC′=√x2+4a2.
Xét ΔAHC′ vuông tại H có: cos(300)=HC′AC′⇔√32=√x2+4a22x2+4a2.
Khi đó: 34=x2+4a22x2+4a2⇔6x2+12a2=4x2+16a2⇔x=a√2.
Thể tích khối trụ có hai đáy là hai đường tròn ngoại tiếp của lăng trụ ABC.A′B′C′ là:
V=πR2h=π(HC)2CC′=π(a√2)2.2a=4πa3.
Đáp án D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai số thực dương a,b. Rút gọn biểu thức ta thu được A=am.bn.
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC vuông tại A,AB=a,BC=2a, mặt bên ACC′A′ là hình vuông. Gọi M,N,P lần lượt là trung điểm của AC,CC′,A′B′ và H là hình chiếu của A lên BC. Tính theo a khoảng cách giữa hai đường thẳng MP và HN.
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y=2−x+3?
Viết phương trình tiếp tuyến của đồ thị hàm số y=2x−1x−2, biết tiếp tuyến có hệ số góc k=−3
Cho hình chữ nhật ABCD có AB=5,BC=4. Tính thể tích của khối lăng trụ tạo thành khi cho hình chữ nhật ABCD quay quanh AB.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−20;2] để hàm số y=x3−x2+3mx−1 đồng biến trên R.
Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong đó có đúng 2 học sinh nam?
Cho số thực dương a khác 1, biểu thức D=loga3a có giá trị bằng bao nhiêu?
Cắt hình nón S bởi một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông cân có cạnh huyền bằng a√2. Tính theo a thể tích của khối nón đã cho.
Cho hình chóp S.ABC có SA⊥(ABC), hai mặt phẳng (SAB) và (SBC) vuông góc với nhau, SB=a√3,^BSC=450,^ASB=300. Thể tích khối chóp SABC là V. Tìm tỉ số a3V.
Cho hàm số y=f(x) liên tục trên đoạn [−2;4] và có đồ thị như hình vẽ.
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;4} \right]\) và có đồ thị như hình vẽ.Phương trình \(3f\left( x \right) - 4 = 0\) có bao nhiêu nghiệm thực trên đoạn \(\ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/04/blobid0-1649620933.png)
Phương trình 3f(x)−4=0 có bao nhiêu nghiệm thực trên đoạn [−2;4]?
Cho hình hộp đứng BACD.A' có đáy là hình thoi cạnh Gọi G là trọng tâm của tam giác góc tạo bởi C'G và mặt đáy bằng {30^0}. Tính theo a thể tích khối hộp
Tìm giá trị lớn nhất của hàm số y = {x^3} - 3{x^2} trên \left[ { - 1;2} \right].
Cho hàm số y = f\left( x \right) xác định trên \mathbb{R}\backslash \left\{ 1 \right\}, liên tục trên mỗi khoảng xác định có bảng biến thiên như sau
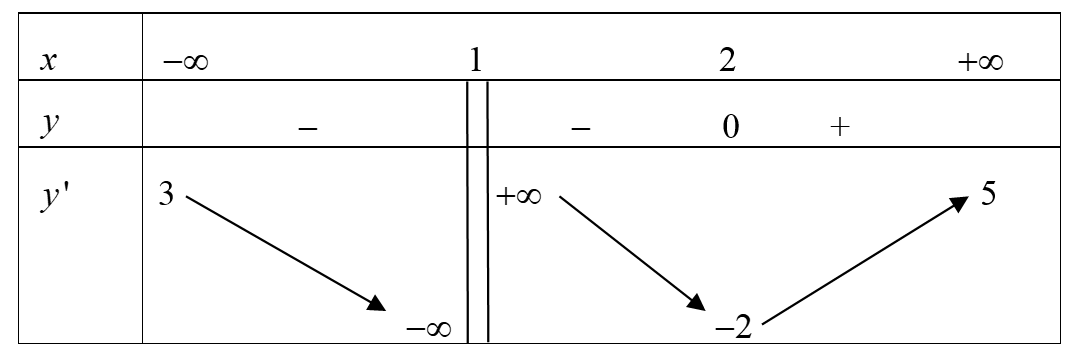
Đồ thị y = \frac{1}{{f\left( x \right) + 2}} có bao nhiêu đường tiệm cận đứng?