Phương trình tiệm cận ngang của đồ thị hàm số $y = \frac{{4 - 3x}}{{4x + 5}}$ là 

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a,SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 .$ Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng

Đường cong ở hình dưới đây là đồ thị của hàm số $y = \frac{{x + a}}{{bx + c}},\left( {a,b,c \in \mathbb{Z}} \right).$ Khi đó giá trị biểu thức $T = a - 3b - 2c$ bằng 

Cho hàm số $y = - {x^3} - 3\left( {m + 1} \right){x^2} + 3\left( {2m - 1} \right)x + 2020.$ Có bao nhiêu giá trị nguyên $m$ để hàm số nghịch biến trên $\left( { - \infty ; + \infty } \right)?$ 

Số đường tiệm cận đứng của đồ thị hàm số $y = \frac{{\sqrt {x + 4} - 2}}{{{x^2} - x}}$ là 

Cho hàm số $f\left( x \right),$ bảng xét dấu của $f'\left( x \right)$ như sau:

  Hàm số $y = f\left( {1 - 2x} \right)$ nghịch biến trên khoảng nào dưới đây?

Hình bát diện đều có bao nhiêu cạnh? 

Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $A,AB = a\sqrt 3 ,AC = a.$ Điểm $A'$ cách đều ba điểm $A,B,C.$ Góc giữa đường thẳng $AB'$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^0}.$ Khoảng cách giữa hai đường thẳng $AA'$ và $BC$ bằng

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,BC = 2a,BA = a\sqrt 3 .$ Biết tam giác $SAB$ vuông tại $A,$ tam giác $SBC$ cân tại $S,\left( {SAB} \right)$ tạo với mặt phẳng $\left( {SBC} \right)$ một góc $\varphi$ thỏa mãn $\sin \varphi = \sqrt {\frac{{20}}{{21}}} .$ Thể tích của khối chóp $S.ABC$ bằng

Cho $x,y,z$ là ba số dương lập thành cấp số nhân; còn ${\log _a}x;{\log _{\sqrt a }}y;{\log _{\sqrt[3]{a}}}z$ lập thành cấp số cộng. Tính giá trị của biểu thức $Q = \frac{{2017x}}{y} + \frac{{2y}}{z} + \frac{z}{x}.$

Gọi $S$ là tập hợp các số tự nhiên có bốn chữ số đôi một khác nhau lập từ các số $0;1;2;3;4;5;6;7.$ Chọn ngẫu nhiên 1 số từ tập hợp $S.$ Tính xác suất để số được chọn có đúng 2 chữ số chẵn.

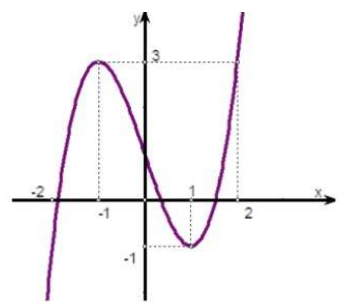
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

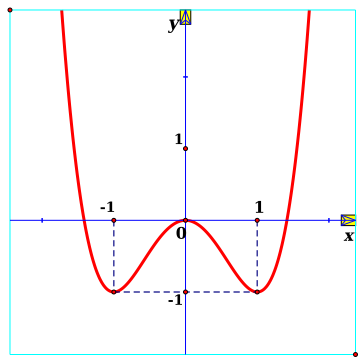
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ:

Gọi $S$ là tập các giá trị nguyên của tham số $m$ để phương trình $f\left( {4\left| {\sin x} \right| + m} \right) - 3 = 0$ có đúng 12 nghiệm phân biệt thuộc nửa khoảng $\left( {0;4\pi } \right].$ Tổng các phần tử của $S$ bằng

Đội văn nghệ của lớp 12A có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn ra 2 học sinh của đội văn nghệ sao cho 2 học sinh có 1 học sinh nam và 1 học sinh nữ.

Cho hàm số $y = \frac{{mx - 18}}{{x - 2m}}.$ Gọi $S$ là tập hợp các giá trị nguyên của tham số $m$ để hàm số đồng biến trên khoảng $\left( {2; + \infty } \right).$ Tổng các phần tử của $S$ bằng

Mặt cầu $\left( S \right)$ có tâm $I$ bán kính $R$ có diện tích bằng