Ba bạn tên Học, Sinh, Giỏi mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn \(\left[ {1;19} \right].\) Tính xác suất để ba số viết ra có tổng chia hết cho 3
A.\(\frac{{3272}}{{6859}}.\)
B.\(\frac{{775}}{{6859}}.\)
C.\(\frac{{1512}}{{6859}}.\)
D. \(\frac{{2287}}{{6859}}.\)
Giải bởi Vietjack
Đáp án D.
Mỗi bạn có 19 cách để viết ra số mình chọn nên không gian mẫu có \(n\left( \Omega \right) = {19^3} = 6859\) cách.
Gọi \(A\) là biến cố 3 số được viết ra của 3 bạn có tổng là một số chia hết cho 3.
Ta đặt \({S_1} = \left\{ {1;4;7;10;13;16;19} \right\}\) là tập hợp các số tự nhiên trong đoạn \(\left[ {1;19} \right]\) khi chia cho 3 thì dư 1.
\({S_2} = \left\{ {2;5;8;11;14;17} \right\}\) là tập hợp các số tự nhiên trong đoạn \(\left[ {1;19} \right]\) khi chia cho 3 thì dư 2.
\({S_3} = \left\{ {3;6;9;12;15;18} \right\}\) là tập hợp các số tự nhiên trong đoạn \(\left[ {1;19} \right]\) chia hết cho 3.
Khi đó biến cố \(A\) xảy ra khi và chỉ khi các số của mỗi bạn viết ra cùng thuộc một tập \({S_i}\left( {i = 1;2;3} \right)\) hoặc ba số của 3 bạn viết ra thuộc về 3 tập phân biệt, khi đó ta có
\(n\left( A \right) = {7^3} + {6^3} + 7.6.6.6 = 2287\) cách
Vậy xác suất để ba số viết ra có tổng chia hết cho 3 là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{2287}}{{6859}}.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \(y = {x^3} - 3{x^2} + mx - 1\) với \(m\) là tham số thực. Tìm tất cả các giá trị của tham số \(m\) để hàm số đạt cực trị tại hai điểm \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 6.\)
Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y = mx - \frac{1}{{{x^3}}} + 2{x^3}\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) là
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(y = f\left( x \right)\) có bao nhiêu cực trị?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ.
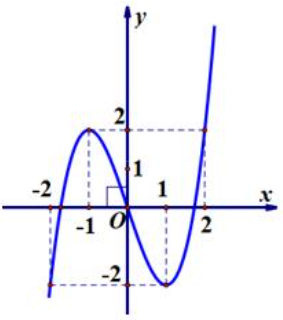
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt {4 + 2f\left( {\cos x} \right)} } \right) = m\) có nghiệm \(x \in \left[ {0;\frac{\pi }{2}} \right).\)
Hình chóp \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 3,BC = 4,SC = 5.\) Tam giác \(SAC\) nhọn và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right).\) Các mặt \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) tạo với nhau một góc \(\alpha \) và \(\cos \alpha = \frac{3}{{\sqrt {29} }}.\) Tính thể tích khối chóp \(S.ABCD\)
Hàm số \(y = {x^3} - 2x,\) hệ thức liên hệ giữa giá trị cực đại \(\left( {{y_{CD}}} \right)\) và giá trị cực tiểu \(\left( {{y_{CT}}} \right)\) là:
Cho \(a,b\) là hai số thực dương bất kì. Mệnh đề nào dưới đây đúng?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA \bot \left( {ABCD} \right),SA = a\sqrt 3 .\) Gọi \(M\) là điểm trên đoạn \(SD\) sao cho \(MD = 2MS.\) Khoảng cách giữa hai đường thẳng \(AB\) và \(CM\) bằng
Cho hình chóp tam giác \(S.ABC\) có đáy là tam giác \(ABC\) đều cạnh có độ dài là \(a,SA\) vuông góc với mặt phẳng đáy, cạnh bên \(SC\) tạo với mặt đáy một góc \({30^0}.\) Thể tích khối chóp
Biết rằng phương trình \({\log _3}\left( {{x^2} - 2020x} \right) = 2021\) có 2 nghiệm \({x_1},{x_2}.\) Tính tổng \({x_1} + {x_2}.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^3}{\left( {x + 1} \right)^2}\left( {x - 2} \right).\) Số điểm cực trị của hàm số đã cho là
Cho hình chóp tứ giác \(S.ABCD\) có đáy là hình vuông cạnh \(AB = a,SA \bot \left( {ABCD} \right)\) và \(SA = a.\) Thể tích của khối chóp \(S.ABCD\) bằng
Phương trình \(\log _2^2x = {\log _2}\frac{{{x^4}}}{2}\) có nghiệm là \(a,b.\) Khi đó \(a.b\) bằng
