Cho các số thực dương \(a,b,x,y\) thỏa mãn \(a >1,b >1\) và \({a^{x - 1}} = {b^y} = \sqrt[3]{{ab}}.\) Giá trị nhỏ nhất của biểu thức \(P = 3x + 4y\) thuộc tập hợp nào dưới đây?
A.\(\left( {7;9} \right].\)
B.\(\left( {11;13} \right).\)
C.\(\left( {1;2} \right).\)
D.\(\left[ {5;7} \right).\)
Giải bởi Vietjack
Đáp án A.
Ta có \({a^{x - 1}} = {b^y} = \sqrt[3]{{ab}} \Leftrightarrow \left[ \begin{array}{l}x = 1 + \frac{1}{3}{\log _a}ab = \frac{4}{3} + \frac{1}{3}{\log _a}b\\y = \frac{1}{3}{\log _b}ab = \frac{1}{3}\left( {1 + {{\log }_b}a} \right) = \frac{1}{3}\left( {1 + \frac{1}{{{{\log }_a}b}}} \right)\end{array} \right..\)
Thay vào \(P,\)ta được
\(P = 3x + 4y = 3\left( {\frac{4}{3} + \frac{1}{3}{{\log }_a}b} \right) + 4.\frac{1}{3}\left( {1 + \frac{1}{{{{\log }_a}b}}} \right)\)
\( = \frac{{16}}{3} + \left( {{{\log }_a}b + \frac{4}{{3{{\log }_a}b}}} \right)\)
Vì \(a >1,b >1\) nên \({\log _a}b >0.\) Áp dụng BĐT Cô-si, ta có:
\(P = \frac{{16}}{3} + \left( {{{\log }_a}b + \frac{4}{{3{{\log }_a}b}}} \right) \ge \frac{{16}}{3} + 2\sqrt {{{\log }_a}b.\frac{4}{{3{{\log }_a}b}}} = \frac{{16 + 4\sqrt 3 }}{3}.\)
Dấu “=” xảy ra khi và chỉ khi \({\log _a}b = \frac{4}{3}{\log _a}b \Leftrightarrow {\log _a}b = \frac{{2\sqrt 3 }}{3}.\)
Vậy giá trị nhỏ nhất của \(P\) bằng \(\frac{{16 + 4\sqrt 3 }}{3} \in \left( {7;9} \right].\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right).\) Biết \(\frac{1}{{{x^2}}}\) là một nguyên hàm của hàm số \(y = f'\left( x \right)\ln x\) và \(f\left( 2 \right) = \frac{1}{{\ln 2}}.\) Khi đó, \(\int\limits_1^2 {\frac{{f\left( x \right)}}{x}dx} \) bằng
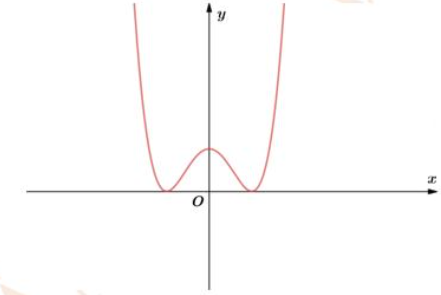
Cho đồ thị hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) như hình vẽ bên. Khẳng định nào sau đây là đúng
Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 5x + 4\) và trục \(Ox.\) Thể tích của khối tròn xoay sinh ra khi quay hình \(\left( H \right)\) quanh trục \(Ox\) bằng:
Gọi \(M,N\) là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3x + 1\) trên \(\left[ {0;2} \right].\) Khi đó \(M + N\) bằng
Cho các số thực \(a,b,c\) thỏa mãn \({a^{{{\log }_3}7}} = 27,{b^{{{\log }_7}11}} = 49,{c^{{{\log }_{11}}25}} = \sqrt {11} .\) Giá trị của biểu thức \(A = {a^{{{\left( {{{\log }_3}7} \right)}^2}}} + {b^{{{\left( {{{\log }_7}11} \right)}^2}}} + {c^{{{\left( {{{\log }_{11}}25} \right)}_2}}}\) là
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng \(2a.\) Thể tích khối trụ bằng
Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( \alpha \right):x + 2y - 1 = 0.\) Vectơ nào sau đây là một vectơ pháp tuyến của \(\left( \alpha \right)?\)
Tập xác định của hàm số \(y = {\log _2}\frac{{x + 3}}{{2 - x}}\) là
Cho tích phân: \(I = \int\limits_1^e {\frac{{\sqrt {1 - \ln x} }}{x}dx} .\) Đặt \(u = \sqrt {1 - \ln x} .\) Khi đó \(I\) bằng
Trong không gian \(Oxyz,\) cho điểm \(A\left( {4; - 1;3} \right)\) và đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{1}.\) Tọa độ điểm \(M\) là điểm đối xứng với điểm \(A\) qua \(d\) là
Cho khối nón có chu vi đáy \(8\pi \) và chiều cao \(h = 3.\) Thể tích khối nón đã cho bằng?
Cho khối lăng trụ có diện tích đáy \(B = 8\) và chiều cao \(h = 6.\) Thể tích của khối lăng trụ đã cho bằng
Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ {1;2} \right],f\left( 1 \right) = 1\) và \(f\left( 2 \right) = 2.\) Khi đó, \(I = \int\limits_1^2 {f'\left( x \right)dx} \) bằng
Trong không gian \(Oxyz,\) cho điểm \(A\left( {1;2;5} \right)\) và mặt phẳng \(\left( P \right):x - 2y + z - 1 = 0.\) Phương trình đường thẳng qua \(A\) vuông góc với \(\left( P \right)\) là:
