Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
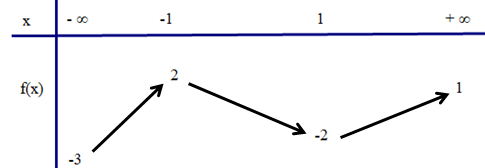
Mệnh đề nào dưới đây đúng?
A. Hàm số không có GTLN và không có GTNN.
B. Hàm số có GTLN bằng \(2\)và GTNN bằng \( - 3.\)
C. Hàm số có GTLN bằng \(2\)và GTNN bằng \( - 2.\)
D. Hàm số có GTLN bằng \(2\)và không có GTNN.
 Giải bởi Vietjack
Giải bởi Vietjack
Từ bảng biến thiên ta thấy hàm số có GTLN bằng 2 và không có GTNN
Đáp án D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Gọi S là tập hợp tất cả các số tự nhiên có 8 chữ số được lập từ các chữ số \(1;2;3;4;5;6\). Lấy ngẫu nhiên một số từ S. Xác suất chọn được số có ba chữ số 1, các chữ số còn lại xuất hiện không quá một lần và hai chữ số chẵn không đứng cạnh nhau bằng
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau
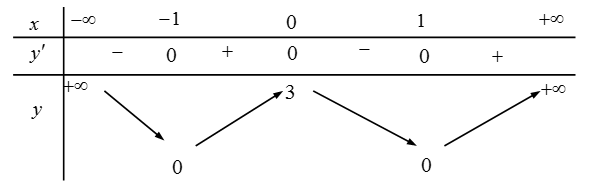
Khẳng định nào sau đây đúng?
Số giá trị nguyên của tham số thực \(m\) để hàm số \(y = \frac{{mx - 2}}{{ - 2x + m}}\) nghịch biến trên khoảng \(\left( {\frac{1}{2};\, + \infty } \right)\) là
Cho đa giác đều có 10 cạnh. Số tam giác có 3 đỉnh là ba đỉnh của đa giác đều đã cho là
Cho hàm số \[f\left( x \right) = {x^3} - 3x + m\] ( với m là tham số thực). Biết \[\mathop {\max }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = 5\] . Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left( {0; + \infty } \right)\)là
Có bao nhiêu giá trị nguyên dương của tham số \(m\) không vượt quá 2020 để hàm số \(y = - {x^4} + (m - 5){x^2} + 3m - 1\) có ba điểm cực trị
Cho hàm số \(f\left( x \right) = a{x^5} + b{x^3} + cx;(a >0;b >0)\) thỏa mãn \(f\left( 3 \right) = - \frac{7}{3};f\left( 9 \right) = 81\). Gọi \[S\] là tập hợp tất cả các giá trị của tham số \[m\] sao cho \[\mathop {\max }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| + \mathop {\min }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| = 86\] với \(g\left( x \right) = f\left( {1 - 2x} \right) + 2.f\left( {x + 4} \right) + m\). Tổng của tất cả các phần tử của \[S\] bằng
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
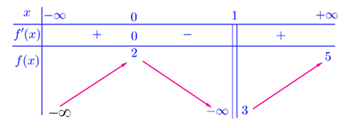
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
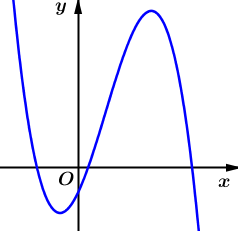
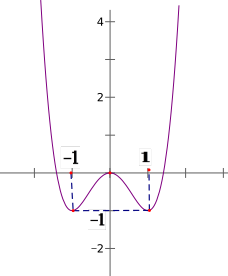
Cho hàm số \(y = f(x) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số \(g(x) = f({x^3} + f(x))\) là
Cho hàm số \[y = \frac{{x + m}}{{x + 1}}\] (\[m\] là tham số thực) thoả mãn \(\mathop {\min }\limits_{\left[ {1;2} \right]} y + \mathop {\max }\limits_{\left[ {1;2} \right]} y = \frac{9}{2}\). Mệnh đề nào dưới đây đúng?
Cho hàm số \(f\left( x \right) = a{x^5} + b{x^3} + cx;(a > 0;b > 0)\) thỏa mãn \(f\left( 3 \right) = - \frac{7}{3};f\left( 9 \right) = 81\). Gọi \[S\] là tập hợp tất cả các giá trị của tham số \[m\] sao cho \[\mathop {\max }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| + \mathop {\min }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| = 86\] với \(g\left( x \right) = f\left( {1 - 2x} \right) + 2.f\left( {x + 4} \right) + m\). Tổng của tất cả các phần tử của \[S\] bằng
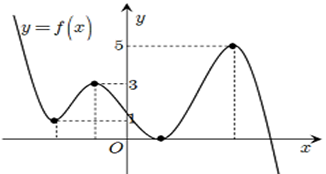
Cho hàm số\(y = f(x)\) liên tục trên\(\mathbb{R}\) và có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\frac{{{m^3} + 5m}}{{\sqrt {{f^2}(x) + 1} }} = {f^2}(x) + 6\) có đúng bốn nghiệm thực phân biệt.
Khối lăng trụ tam giác có độ dài các cạnh đáy lần lượt bằng \(13,14,15\). Cạnh bên tạo với mặt phẳng đáy một góc 300 và có chiều dài bằng 8. Thể tích khối lăng trụ đã cho bằng