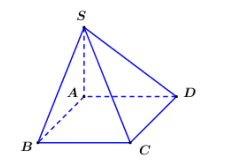
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,SA⊥(ABCD), SA=a√2. Góc giữa đường SC và mặt phẳng (ABCD) bằng
A. 600
B. 900
C. 450
D. 300
Giải bởi Vietjack
Phương pháp:
- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Sử dụng tính chất tam giác vuông cân.
Cách giải:
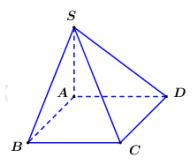
Ta có SA⊥(ABCD)⇒AC là hình chiếu vuông góc của SA lên (ABCD).
⇒∠(SC;(ABCD))=∠(SC;AC)=∠SCA.
Vì ABCD là hình vuông cạnh a nên AC=a√2=SA⇒ΔSAC vuông cân tại A⇒∠SCA=450.
Vậy ∠(SC;(ABCD))=450.
Chọn C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Số giao điểm của đường thẳng y = x + 1 và đồ thị hàm số y=x3−3x+1 là:
Cho hàm số f(x)=2x−mx+2 (m là tham số). Để minx∈[−1;1]f(x)=13 thì m=ab(a∈ℤ,b∈ℕ,b>0). Tổng a + b bằng
Cho tích phân 1∫0x√3x2+1dx nếu đặt u=√3x2+1 thì 1∫0x√3x2+1dx bằng
