Cho f(x) là hàm số bậc ba thỏa mãn f(0) = 2 và f'(1) = 0. Hàm số f'(x) có bảng biến thiên như sau:
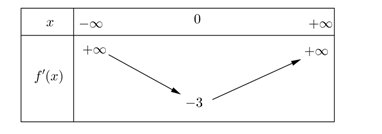
Hàm số có bao nhiêu điểm cực trị?
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
Giả sử
Ta có
Dựa vào bảng biến thiên, ta suy ra đồ thị hàm số f'(x) đối xứng nhau qua trục tung nên là hàm chẵn suy ra b = 0.
Khi đó
Mặt khác cũng từ bảng biến thiến và giả thiết, ta có
Khi đó
Mà .
Vậy
Xét hàm số ta thấy h(x) là một hàm chẵn nên nhận trục tung là trục đối xứng, vì vậy số điểm cực trị của h(x) chính bằng hai lần số cực trị dương của hàm số công thêm 1.
Xét hàm số trên ta có
(do x > 0).
Bảng biến thiên
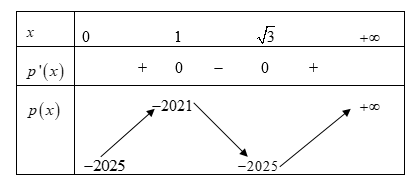
Từ bảng biến thiên, ta suy ra số điểm cực trị của hàm số h(x) là 2.2 + 1 = 5
Mặt khác, đồ thị của hàm số g(x) đối xứng qua Ox, do đó số điểm cực trị của hàm số g(x) bằng số điểm cực trị của hàm số h(x) cộng với số nghiệm bội lẻ của phương trình h(x) = 0.
Dựa vào bảng biến thiên ta có thấy h(x) = 0 có ha nghiệm bội đơn.
Vậy hàm số g(x) có tất cả 5 + 2 = 7 điểm cực trị.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
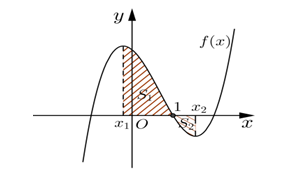
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên dưới f(1) = 0; và . Biết hàm số f(x) đạt cực trị tại hai điểm thỏa mãn . Gọi và là diện tích của hai hình phẳng được gạch trong hình bên dưới. Tỉ số thuộc khoảng nào dưới đây?
Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết cho 3 bằng
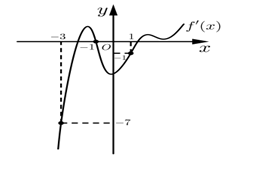
Cho hàm số f(x), đồ thị của hàm số y = f'(x) là đường cong trong hình vẽ bên dưới. Giá trị lớn nhất của hàm số trên đoạn bằng
Cho hàm số y = f(x) có đồ thị trên đoạn [-2; 1] như hình vẽ bên dưới. Giá trị bằng
![Cho hàm số y = f(x) có đồ thị trên đoạn [-2; 1] như hình vẽ bên dưới (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/blobid0-1653271621.png)
Cho hàm số y = f(x) có đạo hàm f'(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và. Tích phân bằng
Trong không gian Oxyz, cho hai mặt phẳng và Giao tuyến của (P) và (Q) có phương trình tham số là