Cho 55∫16dxx√x+9=aln2+bln5+cln11 với a, b, c là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
A. a - b = -c
B. a + b = c
C. a + b = 3c
D. a - b = -3c
Giải bởi Vietjack
Đặt t=√x+9⇒t2=x+9⇒[2tdt=dxx=t2−9
Đổi cận [x=16⇒t=5x=55⇒t=8
⇒55∫16dxx√x+9=8∫52tdt(t2−9)t=28∫5dtt2−9=138∫5(1t−3−1t+3)dt=13ln|t−3||85−13ln|t+3||85
=23ln2+13ln5−13ln11⇒{a=23b=13c=−13⇒a−b=−c.
Chọn A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
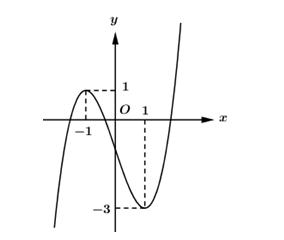
Cho hàm số y = f(x) là hàm đa thức bậc ba có đồ thị như hình vẽ bên dưới. Khẳng định nào sau đây là sai?
Cho hàm số f(x)=x3+(m2+1)x+m2−2 với m là tham số thực. Tìm tất cả các giá trị của 
để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB=2a, AC=3a, AD=4a. Thể tích của khối tứ diện đó là
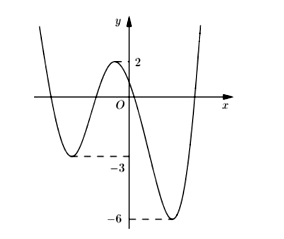
Cho y = f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-12; 12] để hàm số g(x)=|2f(x−1)+m| có 5 điểm cực trị?
Điều kiện cần và đủ để hàm số y=ax4+bx2+c có hai điểm cực đại và một điểm cực tiểu là
Hình nón có đường sinh l = 2a và hợp với đáy góc α=600. Diện tích toàn phần của hình nón bằng
Tìm tất cả các giá trị của m để phương trình 22x−1+m2−m=0 có nghiệm.
Xếp ngẫu nhiên 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C vào sáu ghế quanh một bàn tròn (mỗi học sinh ngồi đúng một ghế). Tính xác suất để học sinh lớp C ngồi giữa 2 học sinh lớp B
Trong không gian Oxyz, cho điểm A(1; 2; 3) và B(3; 4; 7). Phương trình mặt trung trực của đoạn thẳng AB là
