Cho đồ thị hàm số y = f(x) liên tục trên và có đồ thị như hình bên.
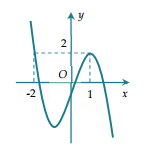
Số nghiệm của phương trình là:
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt t = 1 - f(x) phương trình trở thành f(t) = 2 Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(t) và đường thẳng
y = 2
Dựa vào đồ thị ta thấy phương trình
+ Phương trình f(x) = 0 có 3 nghiệm phân biệt.
+ Phương trình f(x) = 3 có 1 nghiệm.
Và 4 nghiệm này đều phân biệt.
Vậy phương trình đã cho có tất cả 4 nghiệm phân biệt.
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tứ diện ABCD có và Tính khoảng cách d từ A đến mặt phẳng (BCD).
Biết tiếp tuyến của đồ thị hàm số tại điểm A(-1; 1) vuông góc với đường thẳng Tính
Cho hàm số y = f(x) có đạo hàm trên [0; 2]; f(0) = 1 và Tính f(2).
Một hình nón và một hình trụ có cùng chiều cao bằng h và bán kính đường tròn đáy bằng r hơn nữa diện tích xung quanh của chúng cũng bằng nhau. Khi đó, tỉ số bằng:
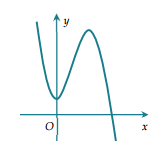
Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
Cho a, b là các số thực dương. Rút gọn biểu thức được kết quả là:
Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 8 quyển sách Tiếng Anh khác nhau được xếp lên một kế sách nằm ngang. Tính xác suất để 2 cuốn sách cùng môn thì không ở cạnh nhau.
Cho hình trụ có chiều cao bằng 4 và nội tiếp trong mặt cầu có bán kính bằng 3. Gọi lần lượt là thể tích của khối trụ và khối cầu đã cho. Tính tỉ số