Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết cùng phương với .
B. M thuộc đoạn FQ với Q là trung điểm của AC;
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A.
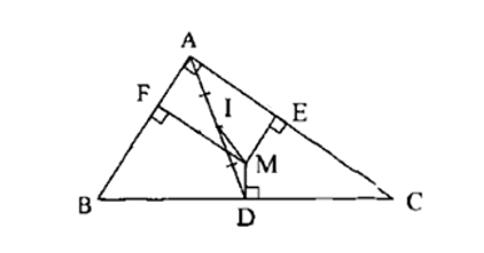
Xét tứ giác AEMF có: .
Do đó, AEMF là hình chữ nhật.
Áp dụng quy tắc hình bình hành ta có: .
Do đó ta có: .
Gọi I là trung điểm của AD.
Khi đó, .
Để cùng phương với thì cùng phương với
Do đó, cùng phương với (do PQ là đường trung bình của tam giác ABC song song với cạnh BC).
Vì M nằm trong tam giác ABC.
Do đó M thuộc đoạn PQ.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: .
Cho tứ giác ABCD và điểm O bất kì sao cho . Tìm điểm M thỏa mãn hệ thức .
Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: .
Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: .
