Cho tập hợp A = {2; 3; 4; 5; 6; 7; 8}. Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập thành từ cách chữ số của tập A. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn mà trong mỗi số luôn có mặt hai chữ số chẵn và hai chữ số lẻ.
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta có : n(Ω) =\(A_7^4\) = 840
Gọi E là biến cố: “ Số được chọn luôn có mặt hai chữ số chẵn và hai chữ số lẻ”
Việc số được chọn luôn có mặt hai chữ số chẵn và hai chữ số lẻ là một công việc gồm 3 công đoạn:
+ Công đoạn 1: Chọn 2 chữ số chẵn từ các chữ số 2; 4; 6; 8 có \(C_4^2\)= 6 cách
+ Công đoạn 2: Chọn 2 chữ số lẻ từ các chữ số 3; 5; 7 có \(C_3^2\)= 3 cách
+ Công đoạn 3: Từ 4 chữ số được chọn ta lập số có 4 chữ số khác nhau, số cách lập tương ứng với một hoán vị của 4 , do đó ta có 4! = 24 cách
⇒ n(E) = 24.6.3 = 432
⇒P(E) = \(\frac{{n(E)}}{{n(\Omega )}}\) = \(\frac{{432}}{{840}}\) = \(\frac{{18}}{{35}}\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Theo kết quả thống kê điểm thi giữa kì 2 môn toán khối 10 của một trường THPT , người ta tính được phương sai của mẫu số liệu đó là s2 = 0,64. Độ lệch chuẩn của mẫu số liệu đó bằng:
Kết quả kiểm tra 15 phút môn toán của 100 học sinh được trình bày ở bảng sau:
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
3 |
5 |
11 |
17 |
30 |
19 |
10 |
5 |
Điểm trung bình môn Toán của các học sinh nói trên là:
Trong một kì thi vấn đáp thí sinh đứng trước ban giám khảo chọn 3 phiếu câu hỏi từ một thùng phiếu gồm 50 câu hỏi, trong đó có 4 cặp phiếu câu hỏi mà mỗi cặp phiếu có nội dung khác nhau từng đôi một và trong mỗi một cặp phiếu có nội dung giống nhau. Tính xác suất để thí sinh chọn được 3 phiếu câu hỏi có nội dung khác nhau.
Số áo bán được trong một quý ở cửa hàng bán áo sơ mi được thống kê như sau:
|
Cỡ áo |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
|
Tần số (số áo bán được) |
13 |
45 |
126 |
125 |
110 |
40 |
12 |
Giá trị mốt của bảng phân bố tần số trên bằng
Cho dãy số liệu thống kê:1; 2; 3; 4; 5; 6; 7. Phương sai của mẫu số liệu trên là
Một Chi Đoàn có 3 Đoàn viên nữ và một số Đoàn viên nam.Cần lập một đội thanh niên tình nguyện (TNTN) gồm 4 người. Gọi A là biến cố :” 4 người được chọn có 3 nữ” và B là biến cố :” 4 người được chọn toàn nam” . Biết rằng P(A) = \(\frac{2}{5}\)P(B). Hỏi Chi Đoàn có bao nhiêu Đoàn viên?
Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bị.Xác suất để chọn được hai viên bi khác màu là:
Cho tam giác ABC có độ dài ba cạnh:
a = 13cm ± 0,2cm; b = 11, 2cm ± 0,2cm; c = 7cm ± 0,1cm. Tính chu vi P của tam giác đã cho.
Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Chọn ngẫu nhiên từ hộp 4 viên bi, tính xác suất để 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh.
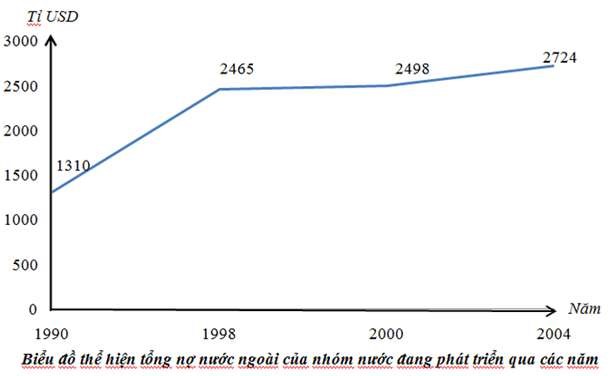
Biểu đồ sau thể hiện tổng nợ nước ngoài của nhóm nước đang phát triẻn trong giai đoạn 1990 đến 2004. Hãy tìm khoảng biến thiên của mẫu số liệu đó.
Cho A và \(\overline A \) là hai biến cố đối nhau. Chọn câu đúng.
Kết quả kiểm tra 15 phút môn toán của 100 học sinh được trình bày ở bảng sau:
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
3 |
5 |
11 |
17 |
30 |
19 |
10 |
5 |
Điểm trung bình môn Toán của các học sinh nói trên là:
Bài tập cuối chương VI
