Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
A. (33; 35).
B. (37; 40).
C. (29; 32).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Từ bảng biến thiên hàm số g(x) = ln f(x) ta có ln f(x) ≥ ln 3, ∀x Î ℝ f(x) ≥ 3, ∀x Î ℝ.
Ta có g'(x) =
Từ bảng biến thiên ta có đồ thị hàm số y = g(x) có 3 điểm cực trị là A(x1; ln30), B(x2; ln 35), C(x3; ln 3) nên f '(x1) = f '(x2) = f '(x3) = 0 và f(x1) = 30, f(x2) = 35, f(x3) = 3.
Do y = f '(x) là hàm số bậc 3 nên phương trình f '(x) = 0 chỉ có tối đa 3 nghiệm x1, x2, x3
Xét phương trình hoành độ giao điểm của f '(x) và g '(x) ta có
f '(x) = g '(x) f '(x) =
.
Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) là:
S =
=
+ Tính I1 = = (do f '(x) ≥ 0, ∀x Î(x1, x2))
Đặt t = f(x) dt = f '(x) dx
Đổi cận:
x = x1 Þ t = f(x1) = 30
x = x2 Þ t = f(x2) = 35
Suy ra I1 = = 35 − ln 35 − 30 + ln30 = 5 + ln .
+ Tính I2 = = (do f '(x) ≥ 0, ∀x Î(x2, x3)).
Đặt t = f(x) dt = f '(x)dx .
Đổi cận
x = x2 Þ t = f(x2) = 35
x = x3 Þ t = f(x3) = 3
Suy ra I2 =
= −(3 − ln 3 − 35 + ln 35) = 32 − ln .
Vậy S = 5 + ln + = 37 +ln ≈ 34,39 Î (33; 35).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?
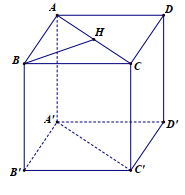
Cho hình lập phương ABCD.A B C D có cạnh bằng 3 ( tham khảo hình bên). Khoảng cách từ B đến mặt phẳng (ACC A) bằng
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Trong không gian Oxyz. Cho hai vectơ = (1; −4; 0) và = (−1; −2; 1). Vectơ + 3 có tọa độ là
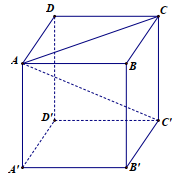
Cho hình lập phương ABCD.A'B'C'D' ( tham khảo hình bên). Giá trị sin của góc giữa đường thẳng AC' và mặt phẳng (ABCD) bằng
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?